数学において、数式は切っても切り離せない存在であり、数式を見やすくを書くことは数学を学ぶうえで極めて重要です。ここでは、数式を見やすく書くことの意義と整式の見やすい書き方を説明します。
数式を見やすく書く意義
数学は数式のもとに成り立つ学問です。基本的にはどの数学の分野においても多かれ少なかれ数式を用います。数式は数学の事象を考察する基礎ですから、わかりやすく表記することがとても重要です。それを実感してもらうために、次の問いに答えてみてください。
(問) 次の整式の次数と定数項を答えよ。
$$\begin{align*}(1)\quad&7532x^3-884x^4+2094x^2-90312+674x^5-8843x\\(2)\quad&4768x^5-91244x^4-215x^3+445x^2+76351x-503\end{align*}$$
解答はこちら
(1) 次数:$5$ 定数項:$-90312$
(2) 次数:$5$ 定数項:$-503$
(1)と(2)、どちらのほうが答えやすかったでしょうか。恐らく、(2)のほうが答えやすかったと思います。なぜでしょうか。2つの式は項の数は同じであり、係数の大きさも大差ありません。大きな違いは、(1)は$x$の次数がバラバラであるのに対し、(2)では次数が大きい順に並んでいる点です。これにより、式の次数を求めるときは一番初めの項を見ればわかりますし、定数項は一番後ろの項を見るだけでわかります。バラバラに並んでいると、いちいち探さなければいけないわけですから、時間のロスになります。たった数秒、と思われるかもしれませんが、この数秒の節約、そしてその数秒間集中する頭の労力の節約が試験では大きな効果を発揮することがよくあるのです。
また、一目で式の特徴がわかるというのは、難しい問題を考察するうえでの手がかりを掴みやすくなるので、数式を整理して書くことは「百利あって一害なし」なのです。
整式の見やすい書き方
それでは、ここからは数式の中でも最も基本的な「整式」に絞って、整式の見やすい書き方を具体的に見ていきます。
ここで一つ注意してほしいことは、今から述べる整理のしかたはいつでも有効なわけではなく、場合によっては異なる整理のしかたをしたほうが都合がいいこともある、ということは頭の片隅に入れておいてください。ただ、大多数の場合において以下の考え方に従って整理をすればキレイに書くことができます。少なくとも、計算結果を整式で示すときには以下に述べる方法で整理をしてから答えるようにしましょう。
降べきの順
まずは、降べきの順です。降べきの順は、各項を次数の大きい方から順に並べる整理のしかたです。詳しくは、こちらを確認してください。
降べきの順に整理することで、整式で最も重要な情報である次数を、先頭の項の次数を読み取るだけで素早く求めることができます。降べきの順は整式を書くときの大原則ですので、必ず意識しましょう。
次数は整式を支配する
整式を降べきの順に整理することで、次数を素早く把握できる!
\(2x^2-3+4x^4-5x^3+6x\)を降べきの順に整理します。
項ごとの次数は順に\(2,\,0,\,4,\,3,\,1\)です。次数が大きい順に項を並べると、\(4x^4\)[4次], \(-5x^3\)[3次], \(2x^2\)[2次], \(6x\)[1次], \(-3\)[0次]となります。よって、降べきの順に並べた式は\(4x^4-5x^3+2x^2+6x-3\)です。
定数を前に、変数を後ろに
続いて、複数種類の文字が登場する場合の考え方です。複数の文字が登場する場合は、まずどの文字が定数で、どの文字が変数かを確認します。そして、定数を前に、変数を後ろに書きます。これは、文字式の書き方のルールである「数は文字よりも前に書く」に則ったものです。ただし、いくら前に書くと言っても普通の数字よりは後ろに書きましょう。
また、円周率の$\pi$や自然対数の底$e$といった、特定の1つの値を指す文字については定数の中でも一番前に書きます。ただし、これについては例外も多く、$\pi$や$e$が後ろに回されることも多いです。このあたりは慣習に依る部分が大きいので、教科書や参考書の書き方を参考にするとよいでしょう。なお、虚数単位$i$は虚数という特殊な数を扱っているため後ろに置くのが普通です。
まとめると、数字 → $\pi$や$e$ → 定数扱いの文字 → 変数扱いの文字 → $i$ という順序で書きます。
$4\times a\times x\times \pi$を整理します。
$a$を定数、$x$を変数とする場合、$4\pi ax$となります。シチュエーションによっては$4a\pi x$や$4ax\pi$が好まれることもあります。一方、$a$を変数、$x$を定数とする場合は$4\pi xa$となります。
アルファベット順
複数種の定数、または複数種の変数が登場する場合は、アルファベット順に書くのが原則です。ただし、特別扱いしたい文字がある場合は、アルファベット順に逆らってそれを前に出すことがあります。
他にも、$w,\,x,\,y,\,z$の4文字を用いる場合は例外的です。アルファベット順に書くならばこの順になります。しかし、数学では変数として真っ先に$x$を使いたがるので、$x$を起点にアルファベット順を考え、$x,\,y,\,z,\,w$という順に並べるのが一般的な慣習となっています。
高校数学ではアルファベットの他にギリシャ文字も登場します。ギリシャ文字にもアルファベットのように順番があるのでそれに従います。高校数学の範囲でよく登場するギリシャ文字の順番は$$\alpha (アルファ) \rightarrow \beta (ベータ) \rightarrow \gamma (ガンマ) \rightarrow \delta (デルタ)(登場頻度はかなり少ない)$$です。また、アルファベットとギリシャ文字が同時に出てくる場合はアルファベットを先に書くことが多いです。($\pi$や$\omega$もギリシャ文字ですが、これらは高校数学範囲では「円周率」や「1の3乗根」といった特別な定数としての登場がほとんどなので、前項に従います。)
$a$と$b$の和は$b+a$よりも$a+b$、積は$ba$よりも$ab$と書くのが一般的です。
複数種の文字が登場する2次以上の多項式
前項は簡単な例を示しましたが、次数が増えてくると整理のしかたも難しくなってきます。基準なくその場の思いつきで整理していると一貫性がなく分かりづらくなるので、以下に示す方法に従って整理することをおすすめします。
文字が2種類の場合と3種類以上の場合で少し考え方が変わってくるので、分けて説明します。まずは文字が2種類の場合です。
- 各項の次数を調べ、大きい順に並べる。
- 次数が同じ項どうしは、アルファベット順が早い文字に着目してその文字の次数が大きい順に並べる。
$a+b^2+a^2b+b^3+4ab+5$を整理します。
項ごとの次数は順に\(1,\,2,\,3,\,3,\,2,\,0\)です。次数が大きい順に項を並べると、\(a^2b,\,b^3\)[3次], \(b^2,\,4ab\)[2次], \(a\)[1次], \(5\)[0次]となります。
3次の項について、アルファベット順が早い$a$に着目すると$a^2b$は2次、$b^3$は0次なので、大きい順に並べると$a^2b,\,b^3$となります。
2次の項も同様に、アルファベット順が早い$a$に着目すると$b^2$は0次、$4ab$は1次なので、大きい順に並べると$4ab,\,b^2$となります。
以上をまとめると、$a^2b+b^3+4ab+b^2+a+5$と整理できます。
続いて、3種類以上の文字を含む場合です。
- 各項の次数を調べ、大きい順に並べる。
- 次数が同じ項どうしは、文字の種類が少ない順に並べる。
- 次数も文字の種類数も同じ項どうしは、アルファベット順が早い文字の次数が大きい順に並べる。
$a^3+a^2b+b^3+bc^2+abc+c^3$を整理します。
すべての項が3次なので、文字の種類が少ない順に並べると、\(a^3,\,b^3,\,c^3\)[1種], \(a^2b,\,bc^2\)[2種], \(abc\)[3種]となります。
文字が1種の項については、まず$a$について3次である$a^3$が初めに来ます。$b^3$と$c^3$はともに$a$については0次ですが、アルファベット順が次に早い$b$について3次である$b^3$が先に来て、0次である$c^3$が後となります。
文字が2種の項については、$a$について2次である$a^2b$が先に、0次である$bc^2$が後になります。
以上をまとめると、$a^3+b^3+c^3+a^2b+bc^2+abc$と整理できます。
なお、少なからず例外も存在します。例えば、$a^2+b^2+c^2+ab$というような式では2通りの整理のしかたがあり、それぞれに利点があります。
- $a^2+b^2+c^2+ab$と整理する。
先に述べた手順通りの整理のしかたです。2乗の項が固まって現れるという利点があります。 - $a^2+ab+b^2+c^2$と整理する。
$a$と$b$が出現する項が固まって現れるという利点があります。
これらはどちらが優れているというものではなく、この式をどのような観点で扱いたいかによって使い分けます。2乗が重要ならば前者の形を用いますし、$a$と$b$だけをまとめて考えたいなら後者の形を使います。
輪環の順
最後に、3種類の文字からなる式で用いられることがある「輪環の順」について説明します。先に輪環の順に整理する例を見てもらいます。
(1)$(a+b)(a+c)(b+c)$を輪環の順に整理すると$(a+b)(b+c)(c+a)$となります。
(2)$(a-b)(a-c)(b-c)$を輪環の順に整理すると$-(a-b)(b-c)(c-a)$となります。
$$\begin{align*}&(a-b)(a-c)(b-c)\\&=(a-b)\cdot \{-(c-a)\}\cdot (b-c)\\&=-(a-b)(b-c)(c-a)\end{align*}$$
(3)$ab+ac+bc$を輪環の順に整理すると$ab+bc+ca$となります。
(4)$a^2b+a^2c+ab^2+ac^2+b^2c+bc^2$を輪環の順に整理すると$a^2b+ab^2+b^2c+bc^2+c^2a+ca^2$となります。($a^2b+b^2c+c^2a+ab^2+bc^2+ca^2$と整理する方法も考えられますが、あまり見かけません。)
上記のように、$a \rightarrow b \rightarrow c \rightarrow a$というように3つの文字が循環するように整理する整理のしかたを「輪環の順」と言います。
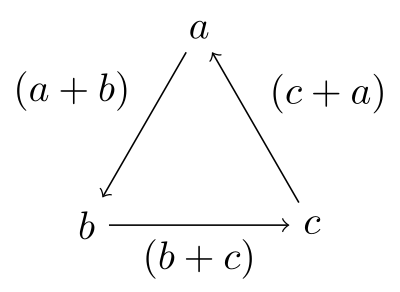
一見するとアルファベット順を崩していてキレイに見えないかもしれませんが、上の図を見るとわかるように、数学において重要な「対称性」を持った配置なので、好んで用いられます。活用の面においても、輪環の順で整理したほうが値の代入などが少しやりやすかったりします。
練習問題
文字式の整理は、慣れていないうちは時間がかかるものです。早めに慣れてサクッと整理できるようになりましょう。
問題
次の式を上述の考え方に基づいて整理せよ。
(1)$5x-6x^3+4-7x^4$
(2)$-6bc^2x+4ax^2-5b+3ac$(ただし、$x$を変数、$a,\,b,\,c$を定数とする)
(3)$x^3-y^3+5xy^2-5x^2y$
(4)$a^2+2ab+2ac+b^2+2bc+c^2$
(5)$ab+ad+bc+cd$
解説
(1) 文字が1種類の式なので、降べきの順に整理すればOKです。
(2) まず、括弧書きの通り$x$が変数で$a,\,b,\,c$は定数であることに注意します。(この問題では練習のために明記していますが、実際は問題文の表現や文字の扱いから変数か定数かを読み取らなければいけません。)降べきの順に整理しますが、$x$のみを変数としているので、$x$のみに着目して降べきの順に整理します。$x$の次数の大きい順に並べると、$4ax^2$[2次],$-6bc^2x$[1次],$-5b,\,3ac$[0次]となります。$x$についてともに0次である$-5b$と$3ac$については、他の文字の次数によって並びを決めます。前者は1次、後者は2次なので後者を先に書きます。
(3) いずれの項も3次なので、アルファベット順の早い$x$の次数に着目して大きい順に並べます。
(4) 3種類の文字が登場する2次の多項式です。まずは各項の次数を調べますが、今回はすべて2次になっています。次に文字の種類が少ない順に並べます。$a^2,\,b^2,\,c^2$は1種類、$2ab,\,2ac,\,2bc$は2種類です。文字が1種類の3項は最終的にアルファベット順に並べることになります。文字が2種類の3項は輪環の順に整理できる組み合わせです。
(5) 先ほど3文字の場合の輪環の順を説明しましたが、実は4文字以上の輪環の順も考えることができます。同じ形の項で文字を$a \rightarrow b \rightarrow c \rightarrow d \rightarrow \cdots \rightarrow a$と並べることができ、余剰な項が出てこない場合は輪環の順に整理するようにします。
解答
$$\begin{align*}(1)&\quad -7x^4-6x^3+5x+4\\(2)&\quad 4ax^2-6bc^2x+3ac-5b\\(3)&\quad x^3-5x^2y+5xy^2-y^3\\(4)&\quad a^2+b^2+c^2+2ab+2bc+2ca\\(5)&\quad ab+bc+cd+da\end{align*}$$
まとめ
- 整式を見やすく整理することは労力の節約や問題解決の糸口を掴むことにつながる
- 数式の整理のしかたは1つに限らないので、状況に適した整理のしかたを考えよう
- 教科書や参考書の数式の書き方は大いに参考にしよう

