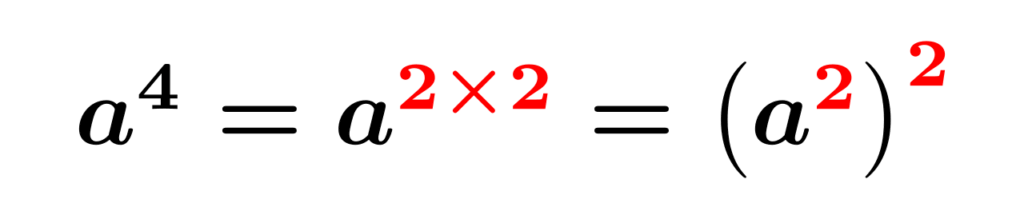ここでは、より高度な因数分解について説明します。
因数分解の手順を再確認
因数分解の手順について再度確認します。
- 共通因数でくくる
- 公式やたすき掛けが利用できないか確認する
- 置き換えによって公式が利用できるようになることもあるので注意
- 複2次式$ax^4+bx^2+c$のパターンに当てはまっているかを確認する
- それぞれの文字の種類ごとに次数を数え、最も次数が小さい文字1つについて降べきの順に整理する
- 係数を共通因数のくくりだしや公式・たすき掛けで因数分解する
- ここまでできたらもう一度手順1からやり直す
これを、それ以上因数分解できない形になるまで繰り返す。
前回の記事では手順1と手順2について説明しました。
この記事では手順3~手順5について説明します。これらを習得すれば、数Ⅰで登場する因数分解はすべて解くことができます。
複2次式の因数分解
まず、複2次式とは何か説明しましょう。といっても、「複2次式」という言葉は高校数学(大学受験数学)の中で使われる用語で、数学全般で見たときにはあまり一般的な語ではありません。なので、複2次式に対する認識は以下の程度で十分です。
$ax^4+bx^2+c\,(a\neq 0)$の形で表される多項式
複2次式の例として、$x^4-10x^2+9$や$x^4+4x^2+16$などが挙げられます。これらの式の因数分解について見ていきます。
これらの式を見たときにまず感じてほしいことが「$x^2$をかたまりに見ることができるぞ!」ということです。指数法則より、$x^4=x^{2\times 2}=(x^2)^2$とできます。わかりやすく、$t=x^2$と置き換えてみると、
\begin{align*}&\hspace{1.3em}x^4-10x^2+9\\&=(x^2)^2-10x^2+9\\&=t^2-10t+9\end{align*}
となります。
なお、置き換えをするとわかりやすくはありますが、置き換えの手間や今後の学習効率を考えると置き換えをせず、$(x^2)^2-10x^2+9$の状態の式で頭の中で$x^2$をかたまりと見て処理できるようになりたいです。
さて、複2次式の因数分解には大きく2種類あります。1つは、かたまりの処理によってすぐに公式を利用できる場合です。$x^4-10x^2+9$はこの例に当てはまります。
\begin{align*}&\hspace{1.3em}x^4-10x^2+9\\&=(x^2)^2-10x^2+9\\&=(x^2-1)(x^2-9)\\&=(x+1)(x-1)(x+3)(x-3)\end{align*}
こちらの場合は、公式さえ理解できていれば、置き換えというステップが挟まるだけなので大して難しくないでしょう。公式が不安な方は、必ず戻って再確認してください。
もう1つの場合がこの項で重点的に扱いたいテーマとなります。$x^4+4x^2+16$を例に見ていきます。この式は$(x^2)^2+4x^2+16$というかたまりで見ることができます。これを因数分解するには、和が$4$で積が$16$である2つの数が欲しいですが、少し考えてみるとわかるように、有理数の範囲でそのような数を見つけることはできません。困りました。
ところで、もし$x^4+8x^2+16$という式であれば、$a^2+2ab+b^2=(a+b)^2$を利用して$x^4+8x^2+16=(x^2+4)^2$と因数分解することができます。この式と$(x^2)^2+4x^2+16$を比べると、2次の係数だけが異なります。このことを利用できないでしょうか。
実は、以下のようにすることで、$x^4+4x^2+16$を因数分解できてしまいます。
$$\begin{align*}&\hspace{1.3em}x^4+4x^2+16\\&=x^4+8x^2+16-4x^2\\&=(x^2+4)^2-(2x)^2\\&=\{(x^2+4)+2x\}\{(x^2+4)-2x\}\\&=(x^2+2x+4)(x^2-2x+4)\end{align*}$$
2行目で$(a+b)^2$の形に変形できる$x^4+8x^2+16$という式を無理やり作ります。ただし、前後の式が等しくないと困るので、$-4x^2$を付け加えることで等号を成り立たせます。これにより、前半は$(x^2+4)^2$という2乗の形が作り出せました。さらに、後から加えた$-4x^2$は$-(2x)^2$と変形できるので、$a^2-b^2=(a+b)(a-b)$という公式の形になっています。これを適用することで、因数分解が完成するのです。
このパターンの因数分解について、手順を整理します。
- $x^2$をかたまりと見て、公式が使えるかを確認。
- 使えるならその公式でそのまま因数分解
- 与えられた式から無理やり作り出せそうな$(a+b)^2$や$(a-b)^2$の形の式を想像する。
- 4次の項と定数項はそのままにして、2次の項だけをいじって作り出せそうなものを考える
- 想像した式の形になるように、2次の項を足し引きで調整。
- 公式$a^2-b^2=(a+b)(a-b)$の形に変形できれば、因数分解できる。
手順2のように、都合のいいように数や式を足し引きすることで問題を考えやすくなることがあります。大事な考え方なので、身につけておきましょう。
都合よく 自分で足し引き
式を与えられたままの形でだけ見ていても世界は広がらない!
自分にとって嬉しい形に積極的に変形しよう!
例で確認しましょう。
(1) $x^4+5x^2+9$を因数分解します。
複2次式の形ですが、和が$5$で積が$9$となる2つの有理数の組は見つからないので、直接公式で因数分解することはできません。
無理やり作り出せそうな$(a+b)^2$や$(a-b)^2$の形の式を考えてみましょう。この2つの式が現れる因数分解の公式を下に示します。
\begin{align*}a^2+2ab+b^2&=(a+b)^2\\a^2-2ab+b^2&=(a-b)^2\end{align*}
いずれにも$a^2,\,b^2$が含まれています。これがそれぞれ$x^4$と$9$にあたることになります。よって、$a=x^2,\,b=3$となり、$(x^2+3)^2$または$(x^2-3)^2$のどちらかを作ることになります。
$(x^2+3)^2$を作る場合を考えます。展開すると$x^4+6x^2+9$となるので、これを$x^4+5x^2+9$に等しくさせるために$-x^2$を加えます。
\begin{align*}&\hspace{1.3em}x^4+5x^2+9\\&=x^4+6x^2+9-x^2\\&=(x^2+3)^2-x^2\end{align*}
すると、ちょうど2乗-2乗の形になっているので、公式通り因数分解します。
\begin{align*}&\hspace{1.3em}x^4+5x^2+9\\&=x^4+6x^2+9-x^2\\&=(x^2+3)^2-x^2\\&=\{(x^2+3)+x\}\{(x^2+3)-x\}\\&=(x^2+x+3)(x^2-x+3)\end{align*}
$(x^2-3)^2$を作る場合も試しておきます。展開すると$x^4-6x^2+9$となるので、これを$x^4+5x^2+9$に等しくさせるために$11x^2$を加えます。
\begin{align*}&\hspace{1.3em}x^4+5x^2+9\\&=x^4-6x^2+9+11x^2\\&=(x^2-3)^2-(\sqrt{11\,}x)^2\end{align*}
見ての通り、2乗-2乗の形にするには根号を使わなければならない状態となりました。係数に実数すべてを使える場合は因数分解できますが、通常は係数が有理数の範囲で考えるので、これは失敗とします。先程の$(x^2+x+3)(x^2-x+3)$が答えとなります。
(2) $4x^4-36x^2+25$を因数分解します。
$x^2$をかたまりで見るとたすき掛けをしたくなる形ですが、残念ながら上手く成功するたすき掛けを見つけることはできません。(各自で確認)
$4x^4=(2x^2)^2,\,25=5^2$なので、$(2x^2+5)^2$か$(2x^2-5)^2$のどちらかを作りに行きます。$(2x^2+5)^2$を作る場合、展開すると$4x^4+20x^2+25$なので、元の式と等しくするには$-56x^2$を加える必要があります。しかし、$56x^2$は有理数係数の範囲で何かの2乗の形にすることができないので、うまくいきません。対して、$(2x^2-5)^2$を作る場合、展開すると$4x^4-20x^2+25$なので、元の式と等しくするには$-16x^2$を加えます。これは、$-(4x)^2$なので、2乗-2乗の形にすることができます。
\begin{align*}&\hspace{1.3em}4x^4-36x^2+25\\&=4x^4-20x^2+25-16x^2\\&=(2x^2-5)^2-(4x)^2\\&=\{(2x^2-5)+4x\}\{(2x^2-5)-4x\}\\&=(2x^2+4x-5)(2x^2-4x-5)\end{align*}
以上が複2次式の因数分解のしかたです。なお、高校数学では殊更$ax^4+bx^2+c$という形が頻出しますが、考え方自体はこの形以外の式にも応用できます。意欲ある人は是非次の$\mathrm{THINK}$も考えてみてください。
次の式を因数分解せよ。
\begin{align*}(1)\quad&x^8+x^4+1\\(2)\quad&27x^9+9x^3-1\end{align*}
解答はこちら
(1) $x^8=x^{4\times 2}=(x^4)^2$なので、$x^4$をひとかたまりと見るのが良さそうです。$x^2$ではなく$x^4$をかたまりと見るという点以外は普通の複2次式と同じ方法で因数分解できます。
\begin{align*}&\hspace{1.3em}x^8+x^4+1\\&=x^8+2x^4+1-x^4\\&=(x^4+1)^2-(x^2)^2\\&=\{(x^4+1)+x^2\}\{(x^4+1)-x^2\}\\&=(x^4+x^2+1)(x^4-x^2+1)\\&=(x^4+2x^2+1-x^2)(x^4-x^2+1)\\&=\{(x^2+1)^2-x^2\}(x^4-x^2+1)\\&=\{(x^2+1)+x\}\{(x^2+1)-x\}(x^4-x^2+1)\\&=(x^2+x+1)(x^2-x+1)(x^4-x^2+1)\end{align*}
一度因数分解ができても安心せず、さらなる因数分解ができないか必ず確認しましょう!
(2) $x^9=x^{3\times 3}=(x^3)^3$なので、$x^3$をひとかたまりとして見ます。すると、与えられた式は$x^3$の3次式として見ることができます。よって、3次式の因数分解の公式を使うことになりそうです。与式の符号にも注意すると、$$a^3-3a^2b+3ab^2-b^3=(a-b)^3$$が利用できそうです。$a=3x^3,\,b=1$と考えると、$a^3=(3x^3)^3=27x^9$と$3ab^2=3\cdot 3x^3\cdot 1^2=9x^3$と$-b^3=-1^3=-1$といった項は与式にありますが、$-3a^2b=-3\cdot (3x)^2 \cdot 1=-27x^6$にあたる項がありません。したがって、この項を補うように変形することを考えます。
\begin{align*}&\hspace{1.3em}27x^9+9x^3-1\\&=27x^9-27x^6+9x^3-1+27x^6\\&=(3x^3-1)^3+27x^6\end{align*}
すると、$27x^6=(3x^2)^3$なので、「3乗+3乗」の公式で更に変形することができます。
\begin{align*}&\hspace{1.3em}27x^9+9x^3-1\\&=(3x^3-1)^3+27x^6\\&=(3x^3-1)^3+(3x^2)^3\\&=\{(3x^3-1)+3x^2\}\{(3x^3-1)^2-(3x^3-1)\cdot 3x^2+(3x^2)^2\}\\&=(3x^3+3x^2-1)\{(9x^6-6x^3+1)-(9x^5-3x^2)+(9x^4)\}\\&=(3x^3+3x^2-1)(9x^6-9x^5+9x^4-6x^3+3x^2+1)\end{align*}
文字が複数種ある式の因数分解
高校数学では、文字が2種類3種類と出てくることは日常のことになります。よって、そのようなたくさんの文字が出てくる複雑な式も手早く処理できるようにならなければなりません。その第一歩として、複数種の文字が登場する多項式の因数分解について考えていきます。
その際に重要となるのが、最初にも触れた因数分解の手順です。特に、手順4と手順5を重点的に練習していきます。
- 共通因数でくくる
- 公式やたすき掛けが利用できないか確認する
- 置き換えによって公式が利用できるようになることもあるので注意
- 複2次式$ax^4+bx^2+c$のパターンに当てはまっているかを確認する
- それぞれの文字の種類ごとに次数を数え、最も次数が小さい文字1つについて降べきの順に整理する
- 係数を共通因数のくくりだしや公式・たすき掛けで因数分解する
- ここまでできたらもう一度手順1からやり直す
これを、それ以上因数分解できない形になるまで繰り返す。
具体的に見ていきます。
(1) $14x^2-12y^2+13xy+18yz+12zx$を因数分解します。
共通因数でくくったり、公式を使ったりすることはできなさそうな式です。また、複2次式の形でもありません。手順1~3では変形できなかったので、手順4に移ります。この式には$x,\,y,\,z$の3種類の文字が出てきますが、それぞれの文字について次数を数えると、$x$については2次式、$y$についても2次式、$z$については1次式です。一般に、次数が小さいほど多項式として単純になります。よって、この式を$z$についての多項式と見ます。
$z$について降べきの順にすると、$(12x+18y)z+(14x^2+13xy-12y^2)$となります。ここまでが手順4です。
ここから、手順5に移ります。つまり、係数の因数分解をします。まず、$z$の1次の係数$12x+18y$は、因数分解すると$6(2x+3y)$となります。次に、定数項はたすき掛けを利用して$$14x^2+13xy-12y^2=(2x+3y)(7x-4y)$$と因数分解できます。ここまでをまとめると、以下の通りです。
\begin{align*}&\hspace{1.3em}14x^2-12y^2+13xy+18yz+12zx\\&=(12x+18y)z+(14x^2+13xy-12y^2)\\&=6(2x+3y)z+(2x+3y)(7x-4y)\end{align*}
手順5まで完了したので、再び手順1に戻ります。上の式を見ると、$2x+3y$が共通因数になっていることがわかるので、これでくくります。
\begin{align*}&\hspace{1.3em}14x^2-12y^2+13xy+18yz+12zx\\&=6(2x+3y)z+(2x+3y)(7x-4y)\\&=(2x+3y)\{6z+(7x-4y)\}\end{align*}
これ以上は因数分解できないので、形を整えて完成です。
\begin{align*}&\hspace{1.3em}14x^2-12y^2+13xy+18yz+12zx\\&=(12x+18y)z+(14x^2+13xy-12y^2)\\&=6(2x+3y)z+(2x+3y)(7x-4y)\\&=(2x+3y)\{6z+(7x-4y)\}\\&=(2x+3y)(7x-4y+6z)\end{align*}
(2) $2x^2y^3-xy^4+10x^2y+3xy^2-4y^3+40x-20y$を因数分解します。
やはり、共通因数でくくったり公式を利用したりするのは困難な式です。文字ごとに次数を数えると、$x$については2次、$y$については4次なので、次数が小さい$x$について降べきの順で整理します。
\begin{align*}&\hspace{1.3em}2x^2y^3-xy^4+10x^2y+3xy^2-4y^3+40x-20y\\&=(2y^3+10y)x^2+(-y^4+3y^2+40)x+(-4y^3-20y)\end{align*}
次に、それぞれの係数を因数分解します。2次の係数は$$2y^3+10y=2y(y^2+5)$$となります。また、定数項は$$-4y^3-20y=-4y(y^2+5)$$となります。1次の係数は$y$の4次の項と2次の項があるので、$y^2$をかたまりとみて考えます。2次の係数と定数項から同じ$y^2+5$という形が出てきているので、1次の係数からも$y^2+5$が出てくるのではないかと思いながら変形するのがポイントです。決めつけは危険ですが、予測を立てて意識して変形することは非常に重要です。
\begin{align*}&\hspace{1.3em}-y^4+3y^2+40\\&=-(y^4-3y^2-40)\\&=-(y^2+5)(y^2-8)\end{align*}
以上をまとめると、$y^2+5$でくくることができます。
\begin{align*}&\hspace{1.3em}2x^2y^3-xy^4+10x^2y+3xy^2-4y^3+40x-20y\\&=(2y^3+10y)x^2+(-y^4+3y^2+40)x+(-4y^3-20y)\\&=2y(y^2+5)x^2-(y^2+5)(y^2-8)x-4y(y^2+5)\\&=(y^2+5)\{2yx^2-(y^2-8)x-4y\}\end{align*}
残された中括弧内の式ですが、よく見るとたすき掛けができます。
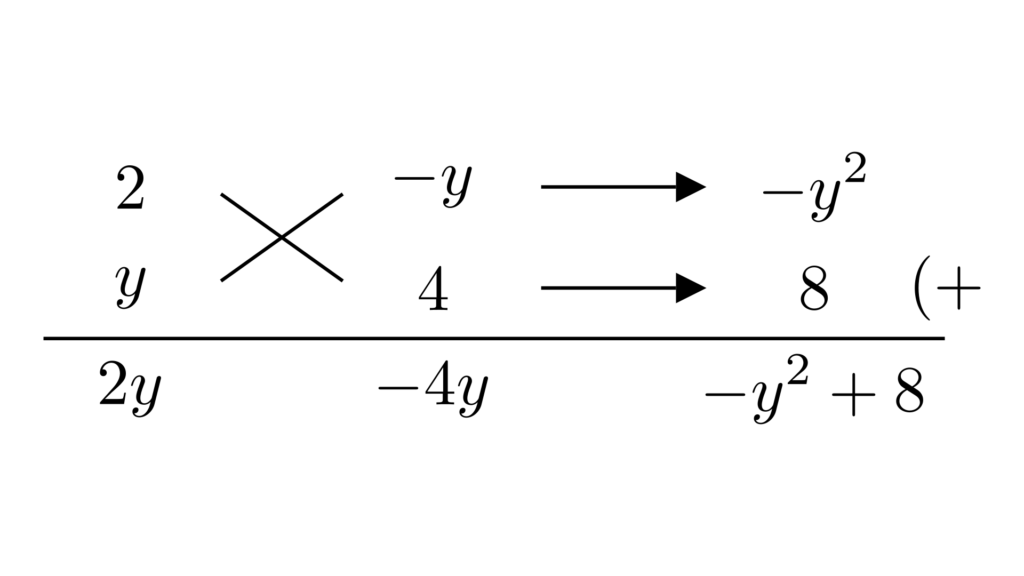
\begin{align*}&\hspace{1.3em}2yx^2-(y^2-8)x-4y\\&=(2x-y)(yx+4)\end{align*}
以上より、因数分解の結果は以下のようになります。
\begin{align*}&\hspace{1.3em}2x^2y^3-xy^4+10x^2y+3xy^2-4y^3+40x-20y\\&=(2y^3+10y)x^2+(-y^4+3y^2+40)x+(-4y^3-20y)\\&=2y(y^2+5)x^2-(y^2+5)(y^2-8)x-4y(y^2+5)\\&=(y^2+5)\{2yx^2-(y^2-8)x-4y\}\\&=(y^2+5)(2x-y)(yx+4)\\&=(2x-y)(xy+4)(y^2+5)\end{align*}
(3) $8x^2+6xy+y^2-2x+2y-15$を因数分解します。
こちらも共通因数の発見や公式の利用は難しいです。よって、次数が小さい方の文字で降べきの順に整理することになりますが、今回の式は$x$についても$y$についても2次式であり、差がありません。このような場合には、最高次の係数が小さい方の文字に着目することでより楽に計算できる場合が多いです。今回は、$x$の2次の係数が$8$であるのに対して、$y$の2次の係数は$1$なので、より小さい$y$について降べきの順に整理します。
\begin{align*}&\hspace{1.3em}8x^2+6xy+y^2-2x+2y-15\\&=y^2+(6x+2)y+(8x^2-2x-15)\end{align*}
続いて、係数を因数分解します。1次の係数は$2$でくくることができますが、この後の工程を考えるとこのまま置いておくほうが手間になりません。定数項はたすき掛けで因数分解しましょう。
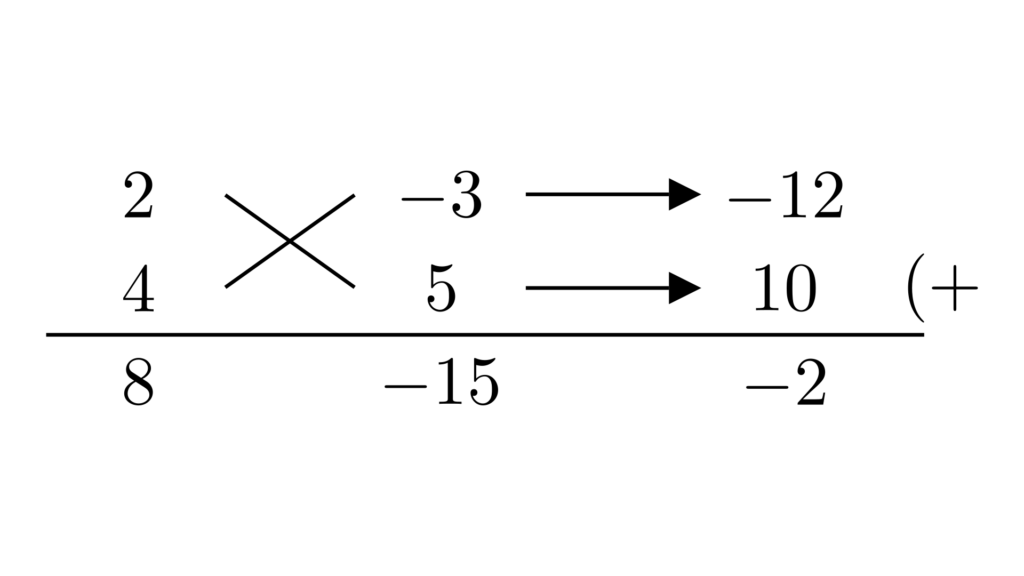
\begin{align*}&\hspace{1.3em}8x^2+6xy+y^2-2x+2y-15\\&=y^2+(6x+2)y+(8x^2-2x-15)\\&=y^2+(6x+2)y+(2x-3)(4x+5)\end{align*}
ここで、改めて式全体を見ると、$y$の2次式として$$y^2+(a+b)y+ab=(y+a)(y+b)$$という公式を用いた因数分解ができそうです。すなわち、和が$6x+2$で積が$(2x-3)(4x+5)$となる2式を考えます。$2x-3$と$4x+5$の2式が適します。(もし、1次の係数$6x+2$を$2$でくくっていると、このタイミングで和を考えるときに分かりづらくなってしまいます。そのため、先程はあえて$2$でくくらずに進めました。)
因数分解の結果は以下のようになります。
\begin{align*}&\hspace{1.3em}8x^2+6xy+y^2-2x+2y-15\\&=y^2+(6x+2)y+(8x^2-2x-15)\\&=y^2+(6x+2)y+(2x-3)(4x+5)\\&=\{y+(2x-3)\}\{y+(4x+5)\}\\&=(2x+y-3)(4x+y+5)\end{align*}
同じ式を$x$で整理してから因数分解すると以下のようになります。文字式絡みのたすき掛けが必要になり、先程より若干面倒です。
\begin{align*}&\hspace{1.3em}8x^2+6xy+y^2-2x+2y-15\\&=8x^2+(6y-2)x+(y^2+2y-15)\\&=8x^2+(6y-2)x+(y-3)(y+5)\\&=\{2x+(y-3)\}\{4x+(y+5)\}\\&=(2x+y-3)(4x+y+5)\end{align*}
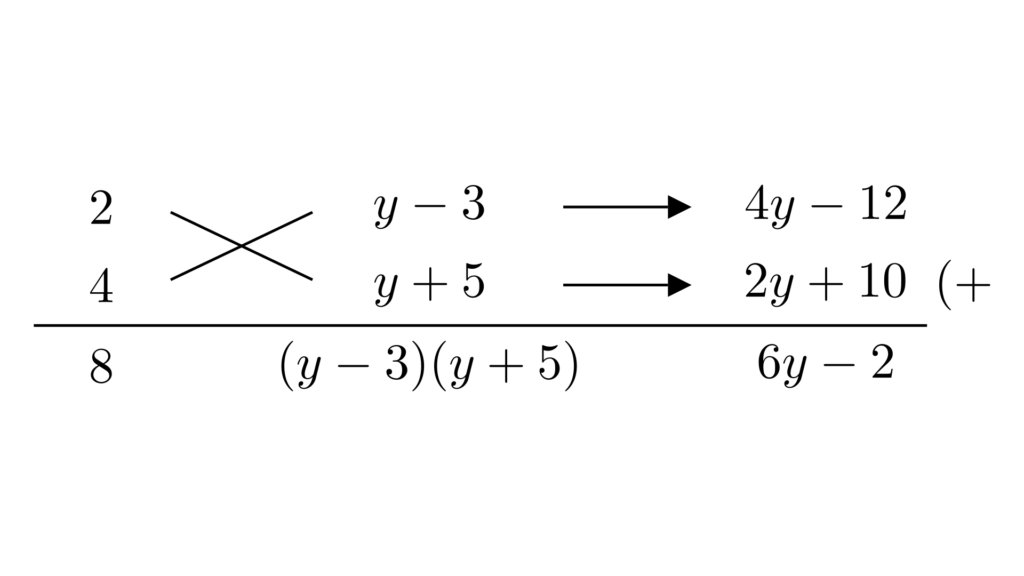
「因数分解の手順」からは逸脱する方法ですが、以下のようにも因数分解できます。
すべての文字について考えて、2次の項($8x^2+6xy+y^2$)と1次の項($-2x+2y$)、そして定数項($-15$)に分けます。2次の項は$$8x^2+6xy+y^2=(2x+y)(4x+y)$$と因数分解できます。さらに、式全体をたすき掛けで因数分解します。
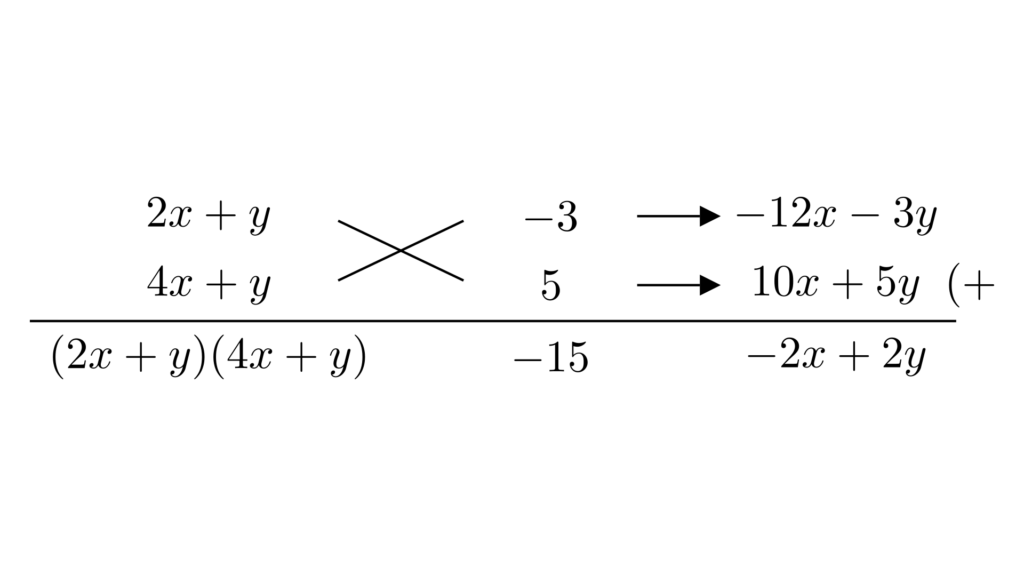
\begin{align*}&\hspace{1.3em}8x^2+6xy+y^2-2x+2y-15\\&=(2x+y)(4x+y)+(-2x+2y)-15\\&=(2x+y-3)(4x+y+5)\end{align*}
$ax^2+bxy+cy^2+dx+ey+f$という形の式を「2元2次式」ということがあります。「2元」とは文字の種類が2種類という意味です。この2元2次式では、上記のような因数分解をすることが可能です
練習問題
問題
次の式を因数分解せよ。$$\begin{align*}(1)\quad&a^4+4a^2+16\\(2)\quad&x^4-14x^2+1\\(3)\quad&9x^4-49x^2y^2+16y^4\\(4)\quad&8x^5+6x^3y^2+18xy^4\\(5)\quad&a^4+4b^4\\(6)\quad&x^2+xy+2yz-4z^2\\(7)\quad&15x^2y+10xy^2-2y^2z-3xyz+60x^2+40xy-8yz-12zx\\(8)\quad&x^2z^2+3xz^2+4xyz+3y^2+2z^2-3xz+5yz-3y-3z\\(9)\quad&a(b+c)^2+b(c+a)^2+c(a+b)^2-3abc\\(10)\quad&3a^2+8ab-3b^2-5a+25b-28\\(11)\quad&28x^2-22xy-30y^2+75x+27y+27\\(12)\quad&3x^2-2y^2-3z^2+5xy-5yz+8zx\end{align*}$$
解説
(1) 与えられた式は複2次式の形になっています。4次の項$a^4$と定数項$+16$に注目すると、$(a^2+4)^2$か$(a^2-4)^2$のどちらかの形を作れそうです。$(a^2+4)^2$を作りに行くと、
\begin{align*}&\hspace{1.3em}a^4+4a^2+16\\&=a^4+8a^2+16-4a^2\\&=(a^2+4)^2-(2a)^2\\&=\{(a^2+4)+2a\}\{(a^2+4)-2a\}\\&=(a^2+2a+4)(a^2-2a+4)\end{align*}
と因数分解ができ、これが答えとなります。一方、$(a^2-4)^2$を作りに行った場合は
\begin{align*}&\hspace{1.3em}a^4+4a^2+16\\&=a^4-8a^2+16+12a^2\\&=(a^2-4)^2-+12a^2\end{align*}
となり、$A^2-B^2$の形にできないので、因数分解できません。
(2) これも複2次式の形です。4次の項$x^4$と定数項$+1$から、$(x^2+1)^2$か$(x^2-1)^2$のどちらかを作りに行きます。$(x^2+1)^2$を作りに行く場合、
\begin{align*}&\hspace{1.3em}x^4-14x^2+1\\&=x^4+2x^2+1-16x^2\\&=(x^2+1)^2-(4x)^2\\&=\{(x^2+1)+4x\}\{(x^2+1)-4x\}\\&=(x^2+4x+1)(x^2-4x+1)\end{align*}
と因数分解することができます。$(x^2-1)^2$を作りに行く場合は、
\begin{align*}&\hspace{1.3em}x^4-14x^2+1\\&=x^4-2x^2+1-12x^2\\&=(x^2-1)^2-(2\sqrt{3}x)^2\end{align*}
となります。$A^2-B^2$の形を作ろうとすると根号が混じってしまい、有理数係数では因数分解することができません。
(3) 文字が$x$と$y$の2種類あり、各項の次数は$x$の4次、$x$の2次と$y$の2次、$y$の4次となっています。次数がこのような組み合わせになっているときは、文字が2種類登場する複2次式の形になっています。$x$の4次の項$9x^4$と$y$の4次の項$16y^4$から、$(3x^2+4y^2)^2$か$(3x^2-4y^2)^2$のどちらかを作りに行きます。$(3x^2+4y^2)^2$を作りに行くと、
\begin{align*}&\hspace{1.3em}9x^4-49x^2y^2+16y^4\\&=9x^4+24x^2y^2+4y^2-73x^2y^2\\&=(3x^2+4y^2)^2-(\sqrt{73}xy)^2\end{align*}
となり、有理数係数の範囲で因数分解することができません。$(3x^2-4y^2)^2$を作りに行くと、
\begin{align*}&\hspace{1.3em}9x^4-49x^2y^2+16y^4\\&=9x^4-24x^2y^2+4y^2-25x^2y^2\\&=(3x^2-4y^2)^2-(5xy)^2\\&=\{(3x^2-4y^2)+5xy\}\{(3x^2-4y^2)-5xy\}\\&=(3x^2+5xy-4y^2)(3x^2-5xy-4y^2)\end{align*}
と因数分解することができます。
(4) まずは共通因数でくくりましょう。各項の係数は偶数なので、$2$でくくることができます。さらに、文字についても、各項に$x$が1つ以上含まれているので$x$でくくることができます。
\begin{align*}&\hspace{1.3em}8x^5+6x^3y^2+18xy^4\\&=2x(4x^4+3x^2y^2+9y^4)\end{align*}
すると、括弧の中に文字が2種類の複2次式の形が現れました。$x$の4次の項$4x^4$と$y$の4次の項$9y^4$から、$(2x^2+3y^2)^2$か$(2x^2-3y^2)^2$のどちらかを作りに行きます。$(2x^2+3y^2)^2$を作りに行くと、
\begin{align*}&\hspace{1.3em}4x^4+3x^2y^2+9y^4\\&=4x^4+12x^2y^2+9y^4-9x^2y^2\\&=(2x^2+3y^2)^2-(3xy)^2\\&=\{(2x^2+3y^2)+3xy\}\{(2x^2+3y^2)-3xy\}\\&=(2x^2+3xy+3y^2)(2x^2-3xy+3y^2)\end{align*}
と因数分解できます。対して、$(2x^2-3y^2)^2$を作りに行くと、
\begin{align*}&\hspace{1.3em}4x^4+3x^2y^2+9y^4\\&=4x^4-12x^2y^2+9y^4+15x^2y^2\\&=(2x^2-3y^2)^2+15x^2y^2\end{align*}
となり、$A^2-B^2$の形にできません。よって、前者の形が正解となり、まとめると
\begin{align*}&\hspace{1.3em}8x^5+6x^3y^2+18xy^4\\&=2x(4x^4+3x^2y^2+9y^4)\\&=2x(4x^4+12x^2y^2+9y^4-9x^2y^2)\\&=2x\{(2x^2+3y^2)^2-(3xy)^2\}\\&=2x\{(2x^2+3y^2)+3xy\}\{(2x^2+3y^2)-3xy\}\\&=2x(2x^2+3xy+3y^2)(2x^2-3xy+3y^2)\end{align*}
となります。
(5) 最初に注意ですが、$a^4\textcolor{red}{-}4b^4$ではなく$a^4\textcolor{red}{+}4b^4$なので直接$A^2-B^2$の公式を使っての因数分解はできません。$a$と$b$が2次ずつの項が抜けた形ですが、これも文字が2種類の複2次式です。$(a^2+2b^2)^2$を作る場合、
\begin{align*}&\hspace{1.3em}a^4+4b^4\\&=a^4+4a^2b^2+b^4-4a^2b^2\\&=(a^2+2b^2)^2-(2ab)^2\\&=\{(a^2+2b^2)+2ab\}\{(a^2+2b^2)-2ab\}\\&=(a^2+2ab+2b^2)(a^2-2ab+2b^2)\end{align*}
と因数分解できます。$(a^2-2b^2)^2$を作る場合、
\begin{align*}&\hspace{1.3em}a^4+4b^4\\&=a^4-4a^2b^2+b^4+4a^2b^2\\&=(a^2-2b^2)^2+4a^2b^2\end{align*}
となり、$A^2-B^2$の形にできません。
$$a^4+4b^4=(a^2+2ab+2b^2)(a^2-2ab+2b^2)$$この等式は、「ソフィー・ジェルマンの恒等式」として知られています。
(6) 複数種の文字が登場するので、それぞれの次数を調べましょう。$x$については2次、$y$については1次、$z$については2次なので、次数が最も小さい$y$について降べきの順に整理します。
\begin{align*}&\hspace{1.3em}x^2+xy+2yz-4z^2\\&=(x+2z)y+x^2-4z^2\end{align*}
続いて、係数を因数分解します。
\begin{align*}&\hspace{1.3em}x^2+xy+2yz-4z^2\\&=(x+2z)y+x^2-4z^2\\&=(x+2z)y+(x+2z)(x-2z)\end{align*}
$x+2z$が共通因数として現れるので、これでくくれば因数分解が完了します。
\begin{align*}&\hspace{1.3em}x^2+xy+2yz-4z^2\\&=(x+2z)y+(x^2-4z^2)\\&=(x+2z)y+(x+2z)(x-2z)\\&=(x+2z)\{y+(x-2z)\}\\&=(x+2z)(x+y-2z)\end{align*}
(7) 気が滅入りそうな長い式ですが、やるべきことは同じです。文字ごとに次数を数えましょう。(もちろん、共通因数がないことや公式が使えないことを先に確認してからです。)$x$と$y$については2次ですが、$z$については1次なので、$z$について降べきの順に整理します。
\begin{align*}&\hspace{1.3em}15x^2y+10xy^2-2y^2z-3xyz+60x^2+40xy-8yz-12zx\\&=(-2y^2-3xy-8y-12x)z+(15x^2y+10xy^2+60x^2+40xy)\end{align*}
次に、係数を因数分解します。$z$の1次の項の係数$-2y^2-3xy-8y-12x$は$x$と$y$を含む式なので、再び次数を数えます。$x$については1次、$y$については2次なので、$x$について降べきの順に整理します。
\begin{align*}&\hspace{1.3em}-2y^2-3xy-8y-12x\\&=(-3y-12)x+(-2y^2-8y)\end{align*}
さらに係数を因数分解すると、共通因数$y+4$が見つかります。
\begin{align*}&\hspace{1.3em}-2y^2-3xy-8y-12x\\&=(-3y-12)x+(-2y^2-8y)\\&=-3(y+4)x-2y(y+4)\\&=-(y+4)(3x+2y)\end{align*}
$z$についての定数項は共通因数をくくるところから始まります。
\begin{align*}&\hspace{1.3em}15x^2y+10xy^2+60x^2+40xy\\&=5x(3xy+2y^2+12x+8y)\end{align*}
括弧の中を、次数が小さい$x$について降べきの順に整理します。
\begin{align*}&\hspace{1.3em}3xy+2y^2+12x+8y\\&=(3y+12)x+(2y^2+8y)\end{align*}
係数を因数分解して、共通因数をくくり出します。
\begin{align*}&\hspace{1.3em}3xy+2y^2+12x+8y\\&=(3y+12)x+(2y^2+8y)\\&=3(y+4)x+2y(y+4)\\&=(y+4)(3x+2y)\end{align*}
以上をまとめると、次のようになります。
\begin{align*}&\hspace{1.3em}15x^2y+10xy^2-2y^2z-3xyz+60x^2+40xy-8yz-12zx\\&=(-2y^2-3xy-8y-12x)z+(15x^2y+10xy^2+60x^2+40xy)\\&=-(y+4)(3x+2y)z+5x(y+4)(3x+2y)\end{align*}
共通因数をくくり出せば、因数分解完了です。
\begin{align*}&\hspace{1.3em}15x^2y+10xy^2-2y^2z-3xyz+60x^2+40xy-8yz-12zx\\&=(-2y^2-3xy-8y-12x)z+(15x^2y+10xy^2+60x^2+40xy)\\&=-(y+4)(3x+2y)z+5x(y+4)(3x+2y)\\&=(y+4)(3x+2y)(-z+5x)\\&=(3x+2y)(5x-z)(y+4)\end{align*}
(8) 今回の式は、$x,\,y,\,z$のいずれについても2次式です。ですので、どの文字で整理しても大きな差はなさそうです。しかし、ここではもう少し吟味してみましょう。仮に$x$について降べきの順に整理したとすると、$x$の2次の項の係数は$z^2$となります。また、$y$について整理した場合は$3$になり、$z$について整理した場合は$x^2+3x+2$となります。一般に、次数が高い項の係数が単純であるほうが式の扱いが楽なことが多いです。よって、ここでは$y$について整理することにします。
「次数が高い項の係数が単純なもの」というのは1つの基準に過ぎません。他の選び方には、例えば、ある文字について2次の項と定数項のみが現れて1次の項が無いような場合は、その文字について整理すれば分類が2種類だけになり、細かく分ける場合よりも共通因数などをあぶり出しやすくなる、という考え方もあります。
与えられた式を$y$についての降べきの順に整理すると次のようになります。
\begin{align*}&\hspace{1.3em}x^2z^2+3xz^2+4xyz+3y^2+2z^2-3xz+5yz-3y-3z\\&=3y^2+(4xz+5z-3)y+(x^2z^2+3xz^2+2z^2-3xz-3z)\end{align*}
2次の係数$3$と1次の係数$4xz+5z-3$は因数分解できないので、定数項の因数分解をします。$z$が共通因数なのでくくり出すと、残された式は$z$について1次になり$x$より次数が小さくなるので、$z$について整理します。
\begin{align*}&\hspace{1.3em}x^2z^2+3xz^2+2z^2-3xz-3z\\&=z(x^2z+3xz+2z-3x-3)\\&=z\{(x^2+3x+2)z+(-3x-3)\}\end{align*}
さらに、係数を因数分解します。
\begin{align*}&\hspace{1.3em}x^2z^2+3xz^2+2z^2-3xz-3z\\&=z\{(x^2+3x+2)z+(-3x-3)\}\\&=z\{(x+1)(x+2)z-3(x+1)\}\end{align*}
共通因数$x+1$をくくり出して整理します。
\begin{align*}&\hspace{1.3em}x^2z^2+3xz^2+2z^2-3xz-3z\\&=z\{(x+1)(x+2)z-3(x+1)\}\\&=z(x+1)\{(x+2)z-3\}\\&=z(x+1)(xz+2z-3)\end{align*}
式全体は次のようになります。
\begin{align*}&\hspace{1.3em}x^2z^2+3xz^2+4xyz+3y^2+2z^2-3xz+5yz-3y-3z\\&=3y^2+(4xz+5z-3)y+(x^2z^2+3xz^2+2z^2-3xz-3z)\\&=3y^2+(4xz+5z-3)y+z(x+1)(xz+2z-3)\end{align*}
この式に共通因数はありません。公式の利用を検討すると、この式は今$y$についての2次式と見ているので、たすき掛けができそうです。2次の係数は$1\times 3$しかありません。定数項は一見すると3式の積で複雑ですが、闇雲に試すのではなく、ありえないパターンを除外すれば組み合わせは限られます。まず、1次の係数に$xz^2$の項がないことから$z$と$xz+2z-3$は一緒になりません。また、1次の係数には$x^2z$の項もないので、$x+1$と$xz+2z-3$も一緒になりません。この2つの事実から$xz+2z-3$は単独で使うしかなく、組み合わせは$z(x+1)\times (xz+2z-3)$のみです。1次の係数の定数項が$-3$であり、$z(x+1)$から定数項が生まれないことを踏まえると、$xz+2z-3$は$1$と掛け合わせるべきです。結果として、以下のようにたすき掛けが成立します。
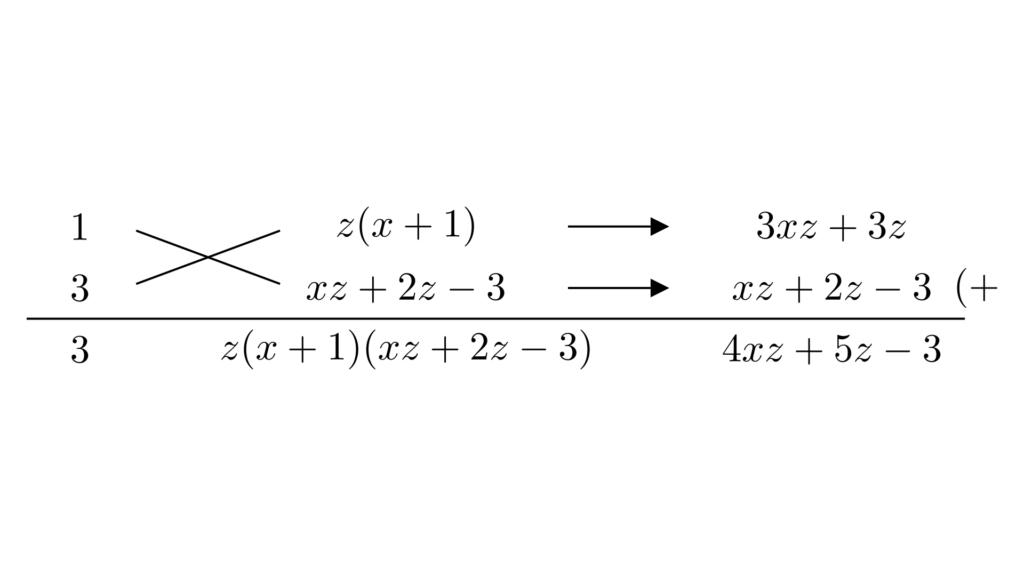
よって、以下のように因数分解ができます。
\begin{align*}&\hspace{1.3em}x^2z^2+3xz^2+4xyz+3y^2+2z^2-3xz+5yz-3y-3z\\&=3y^2+(4xz+5z-3)y+(x^2z^2+3xz^2+2z^2-3xz-3z)\\&=3y^2+(4xz+5z-3)y+z(x+1)(xz+2z-3)\\&=\{y+z(x+1)\}\{3y+(xz+2z-3)\}\\&=(xz+y+z)(xz+3y+2z-3)\end{align*}
参考として、はじめに他の文字で整理した場合も示しておきます。時間に余裕があれば、他の文字で整理しての因数分解も行って、結果が合うか検算するのが良いでしょう。
〈$x$で整理した場合〉
\begin{align*}&\hspace{1.3em}x^2z^2+3xz^2+4xyz+3y^2+2z^2-3xz+5yz-3y-3z\\&=z^2x^2+(3z^2+4yz-3z)x+(3y^2+2z^2+5yz-3y-3z)\\&=z^2x^2+(3z^2+4yz-3z)x+\{3y^2+(5z-3)y+(2z^2-3z)\}\\&=z^2x^2+(3z^2+4yz-3z)x+\{3y^2+(5z-3)y+z(2z-3)\}\\&=z^2x^2+(3z^2+4yz-3z)x+(y+z)(3y+2z-3)\\&=\{zx+(y+z)\}\{zx+(3y+2z-3)\}\\&=(xz+y+z)(xz+3y+2z-3)\end{align*}
〈$z$で整理した場合〉
\begin{align*}&\hspace{1.3em}x^2z^2+3xz^2+4xyz+3y^2+2z^2-3xz+5yz-3y-3z\\&=(x^2+3x+2)z^2+(4xy-3x+5y-3)z+(3y^2-3y)\\&=(x+1)(x+2)z^2+(4xy-3x+5y-3)z+3y(y-1)\\&=\{(x+1)z+y\}\{(x+2)z+3(y-1)\}\\&=(xz+y+z)(xz+3y+2z-3)\end{align*}
(9) 式の一部がすでに括弧でくくられていますが、整式の積の形ではないので因数分解ではありません。このままの形では変形が難しいので、一度展開して括弧を外してしまいましょう。
\begin{align*}&\hspace{1.3em}a(b+c)^2+b(c+a)^2+c(a+b)^2-3abc\\&=a(b^2+2bc+c^2)+b(c^2+2ca+a^2)+c(a^2+2ab+b^2)-3abc\\&=ab^2+2abc+c^2a+bc^2+2abc+a^2b+ca^2+2abc+b^2c-3abc\\&=a^2b+ab^2+b^2c+bc^2+c^2a+ca^2+3abc\end{align*}
展開が終わった式を見てみると、$a,\,b,\,c$のいずれの文字についても2次式になっています。係数の複雑さなども差がないので、どの文字で整理しても大差ないでしょう。ここでは、$c$について整理します。定数項は共通因数をくくり出すことができます。
\begin{align*}&\hspace{1.3em}a(b+c)^2+b(c+a)^2+c(a+b)^2-3abc\\&=a^2b+ab^2+b^2c+bc^2+c^2a+ca^2+3abc\\&=(a+b)c^2+(a^2+3ab+b^2)c+(a^2b+ab^2)\\&=(a+b)c^2+(a^2+3ab+b^2)c+ab(a+b)\end{align*}
共通因数は特に見つからないので、全体を$c$の2次式と見てたすきがけをしましょう。
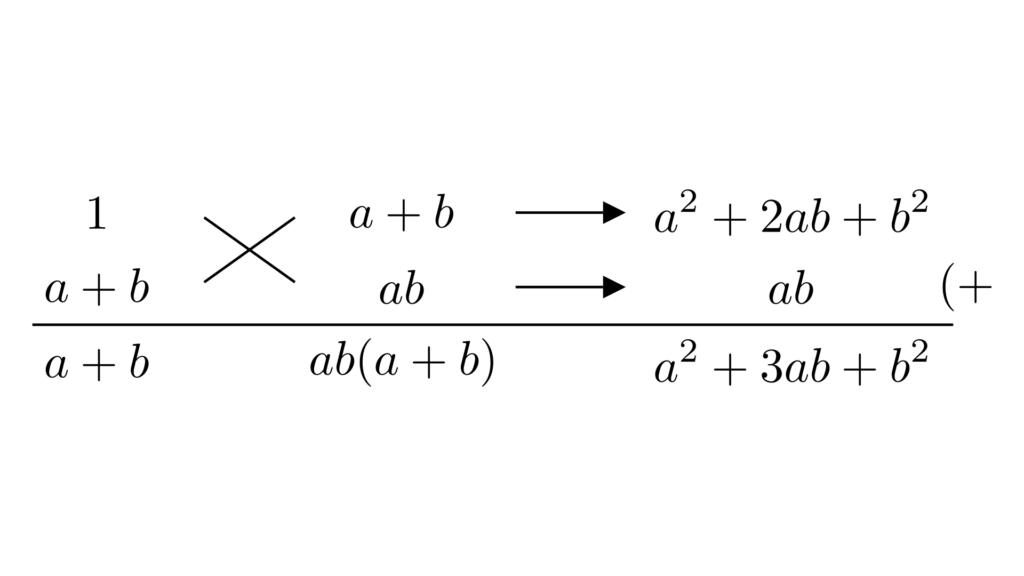
\begin{align*}&\hspace{1.3em}a(b+c)^2+b(c+a)^2+c(a+b)^2-3abc\\&=a(b^2+2bc+c^2)+b(c^2+2ca+a^2)+c(a^2+2ab+b^2)-3abc\\&=ab^2+2abc+c^2a+bc^2+2abc+a^2b+ca^2+2abc+b^2c-3abc\\&=a^2b+ab^2+b^2c+bc^2+c^2a+ca^2+3abc\\&=(a+b)c^2+(a^2+3ab+b^2)c+(a^2b+ab^2)\\&=(a+b)c^2+(a^2+3ab+b^2)c+ab(a+b)\\&=\{c+(a+b)\}\{(a+b)c+ab\}\\&=(a+b+c)(ab+bc+ca)\end{align*}
(10) $a,\,b$のいずれについても2次式なので、どちらで整理してもよいですが、2次の係数を比較すると、$a^2$の係数は$3$で正であるのに対し、$b^2$の係数は$-3$で負です。2次の係数が負だとたすき掛けが少し面倒なので、正である$a$について整理することにします。定数項はたすき掛けのためにマイナスでくくっておきましょう。
\begin{align*}&\hspace{1.3em}3a^2+8ab-3b^2-5a+25b-28\\&=3a^2+(8b-5)a+(-3b^2+25b-28)\\&=3a^2+(8b-5)a-(3b^2-25b+28)\end{align*}
定数項をたすき掛けで因数分解します。
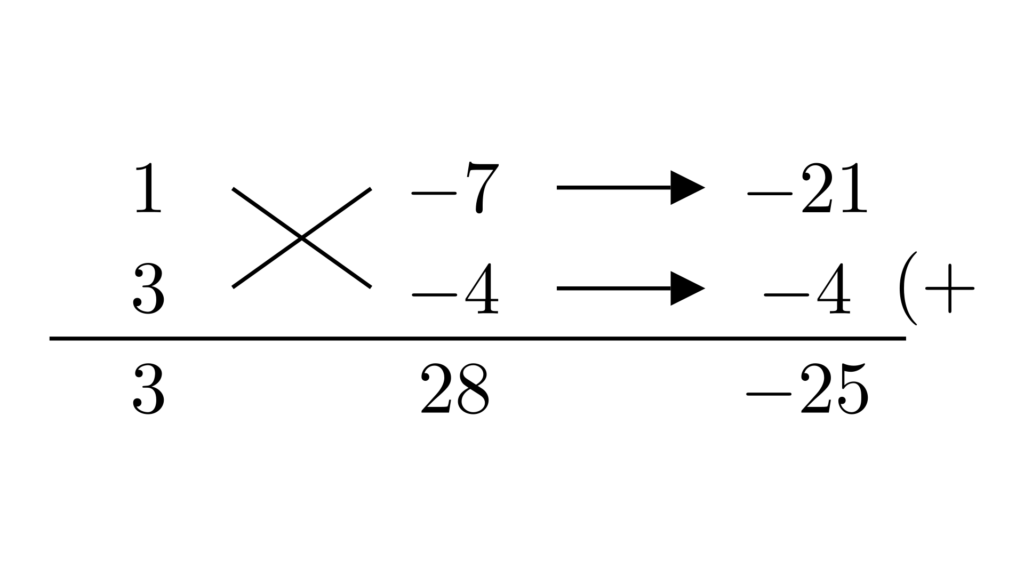
$$3b^2-25b+28=(b-7)(3b-4)$$
\begin{align*}&\hspace{1.3em}3a^2+8ab-3b^2-5a+25b-28\\&=3a^2+(8b-5)a-(3b^2-25b+28)\\&=3a^2+(8b-5)a-(b-7)(3b-4)\end{align*}
続いて、式全体を$a$の2次式として因数分解します。
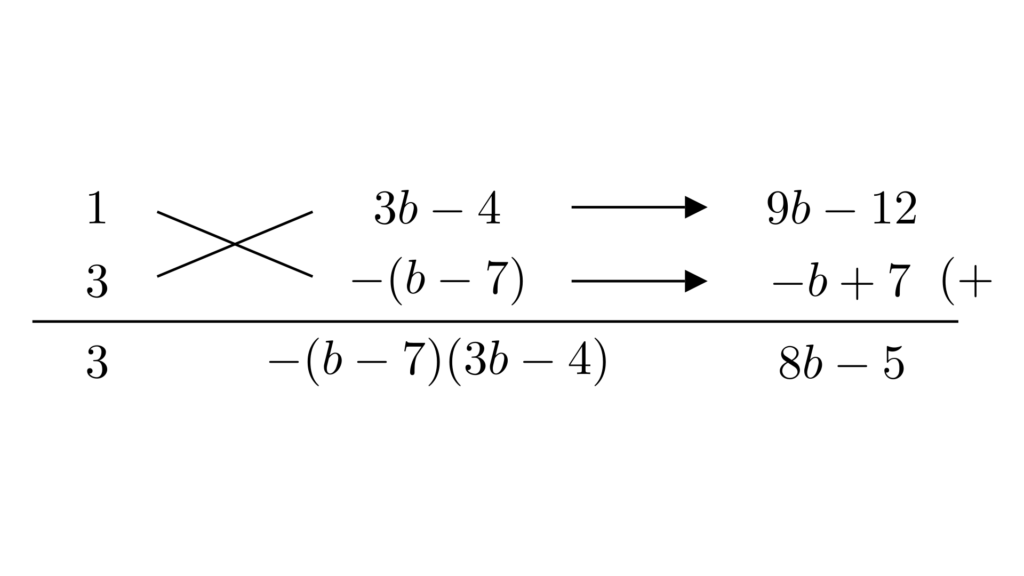
これらより、以下のように因数分解ができます。
\begin{align*}&\hspace{1.3em}3a^2+8ab-3b^2-5a+25b-28\\&=3a^2+(8b-5)a+(-3b^2+25b-28)\\&=3a^2+(8b-5)a-(3b^2-25b+28)\\&=3a^2+(8b-5)a-(b-7)(3b-4)\\&=\{a+(3b-4)\}\{3a-(b-7)\}\\&=(a+3b-4)(3a-b+7)\end{align*}
(11) この式も$x,\,y$のいずれについても2次式です。2次の係数が正である$x$について整理すると、
\begin{align*}&\hspace{1.3em}28x^2-22xy-30y^2+75x+27y+27\\&=28x^2+(-22y+75)x+(-30y^2+27y+27)\end{align*}
となります。定数項は次のように因数分解できます。
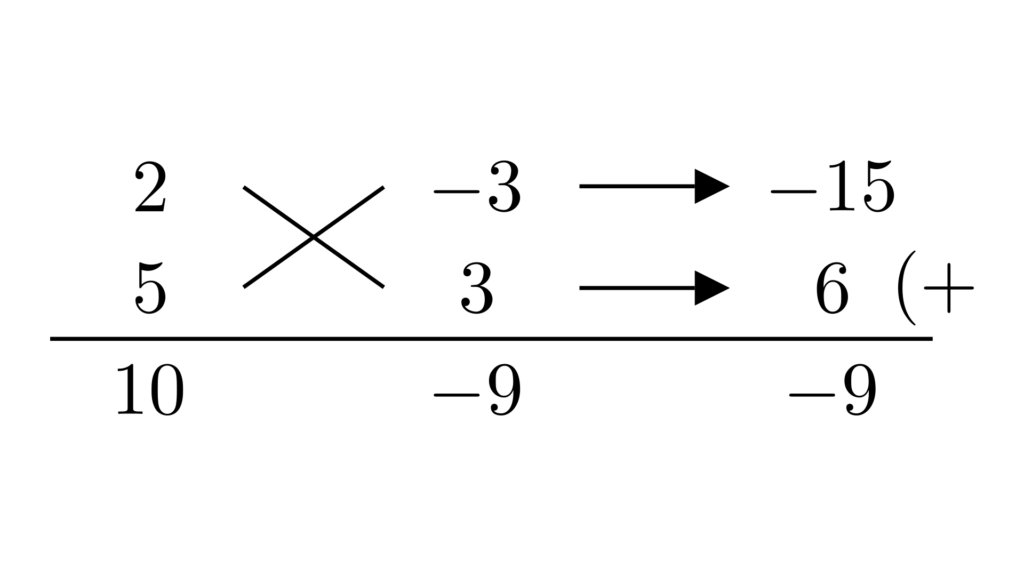
\begin{align*}&\hspace{1.3em}-30y^2+27y+27\\&=-3(10y^2-9y-9)\\&=-3(2y-3)(5y+3)\end{align*}
\begin{align*}&\hspace{1.3em}28x^2-22xy-30y^2+75x+27y+27\\&=28x^2+(-22y+75)x+(-30y^2+27y+27)\\&=28x^2+(-22y+75)x-3(2y-3)(5y+3)\end{align*}
さらに、全体をたすき掛けで因数分解すると、以下のようになります。
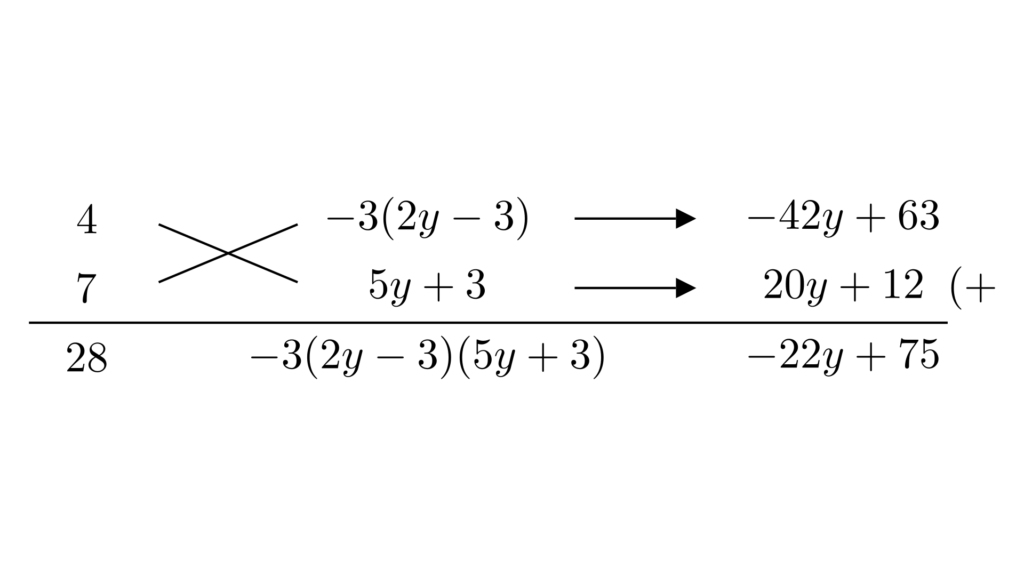
\begin{align*}&\hspace{1.3em}28x^2-22xy-30y^2+75x+27y+27\\&=28x^2+(-22y+75)x+(-30y^2+27y+27)\\&=28x^2+(-22y+75)x-3(2y-3)(5y+3)\\&=\{4x-3(2y-3)\}\{7x+(5y+3)\}\\&=(4x-6y+9)(7x+5y+3)\end{align*}
(12) $x,\,y,\,z$のいずれについても2次式です。ここでも、2次の係数が正である$x$について整理します。
\begin{align*}&\hspace{1.3em}3x^2-2y^2-3z^2+5xy-5yz+8zx\\&=3x^2+(5y+8z)x+(-2y^2-5yz-3z^2)\\&=3x^2+(5y+8z)x-(2y^2+5yz+3z^2)\end{align*}
定数項は次のように因数分解できます。
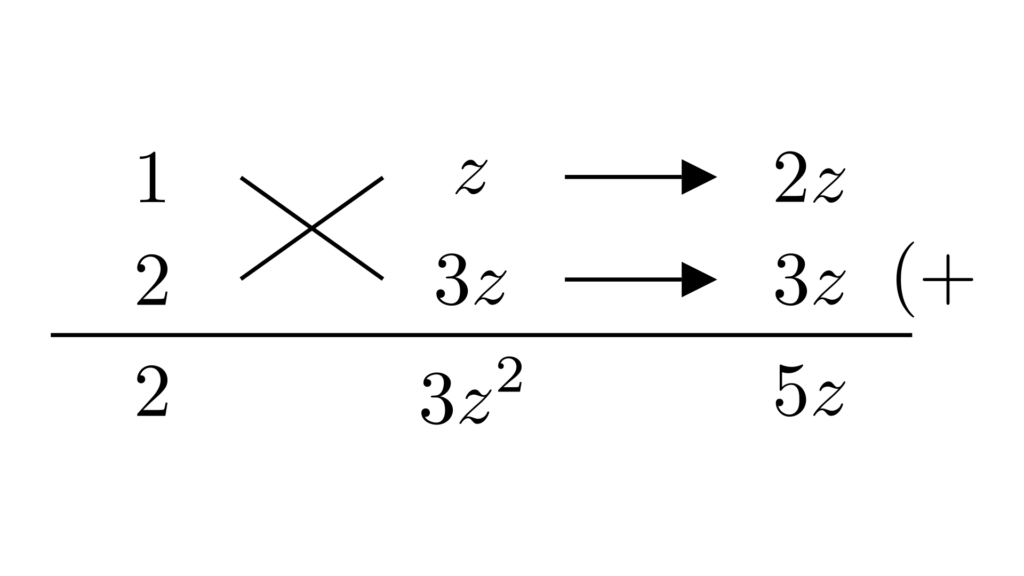
$$2y^2+5yz+3z^2=(y+z)(2y+3z)$$
\begin{align*}&\hspace{1.3em}3x^2-2y^2-3z^2+5xy-5yz+8zx\\&=3x^2+(5y+8z)x-(2y^2+5yz+3z^2)\\&=3x^2+(5y+8z)x-(y+z)(2y+3z)\end{align*}
式全体にたすき掛けを適用して、以下のように因数分解できます。
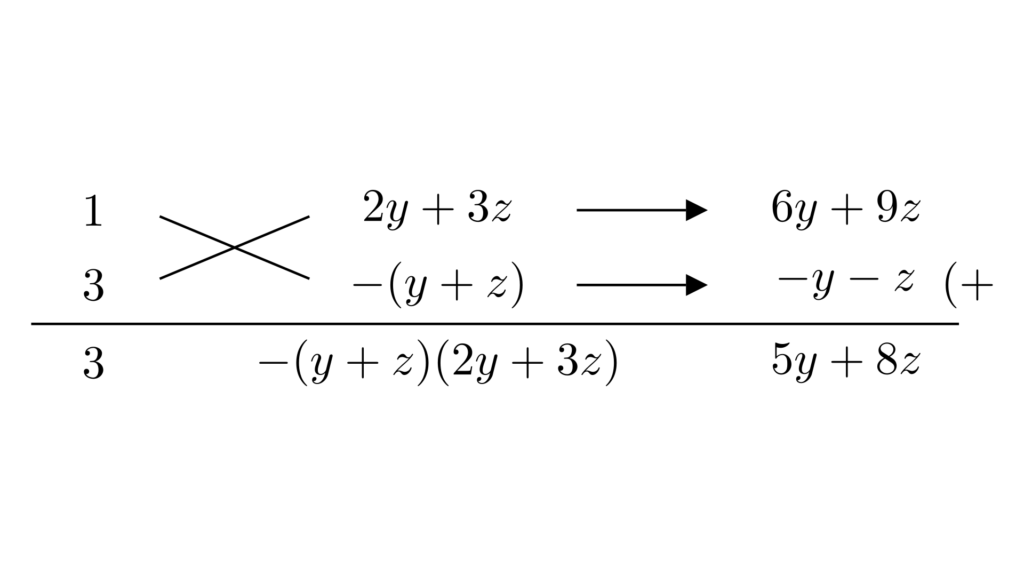
\begin{align*}&\hspace{1.3em}3x^2-2y^2-3z^2+5xy-5yz+8zx\\&=3x^2+(5y+8z)x-(2y^2+5yz+3z^2)\\&=3x^2+(5y+8z)x-(y+z)(2y+3z)\\&=\{x+(2y+3z)\}\{3x-(y+z)\}\\&=(x+2y+3z)(3x-y-z)\end{align*}
解答
$$\begin{align*}(1)\quad&(a^2+2a+4)(a^2-2a+4)\\(2)\quad&(x^2+4x+1)(x^2-4x+1)\\(3)\quad&(3x^2+5xy-4y^2)(3x^2-5xy-4y^2)\\(4)\quad&2x(2x^2+3xy+3y^2)(2x^2-3xy+3y^2)\\(5)\quad&(a^2+2ab+2b^2)(a^2-2ab+2b^2)\\(6)\quad&(x+2z)(x+y-2z)\\(7)\quad&(3x+2y)(5x-z)(y+4)\\(8)\quad&(xz+y+z)(xz+3y+2z-3)\\(9)\quad&(a+b+c)(ab+bc+ca)\\(10)\quad&(a+3b-4)(3a-b+7)\\(11)\quad&(4x-6y+9)(7x+5y+3)\\(12)\quad&(x+2y+3z)(3x-y-z)\end{align*}$$
まとめ
- 4次・2次・定数項のみで構成される整式は複2次式の因数分解を考える
- 整式の次数は小さいほど扱いが楽
- 複数の文字を含む整式は次数が最小の文字で降べきの順に整理