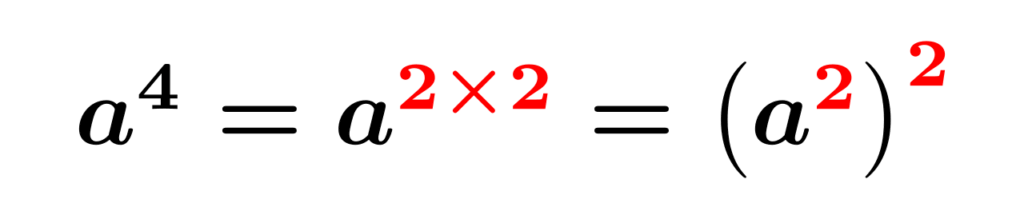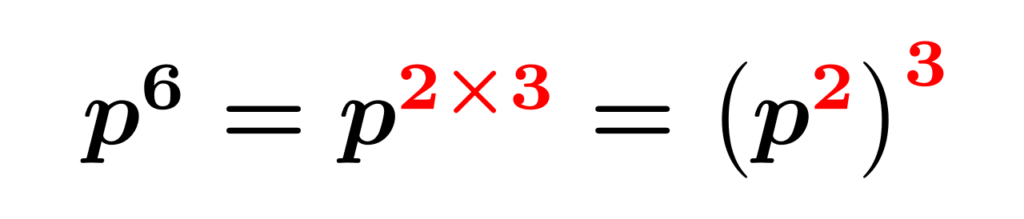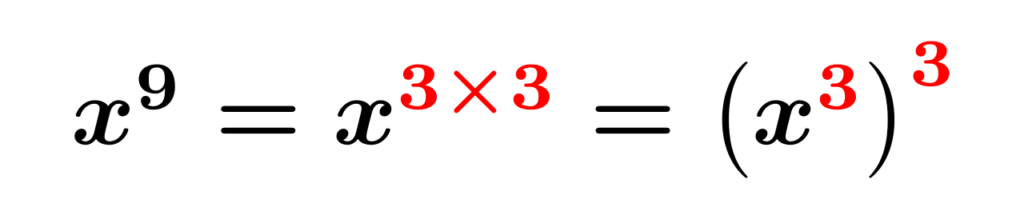ここでは、因数分解の基本と公式を利用した因数分解の方法について説明します。
因数と因数分解
以下の3つの記事では、整式の展開について勉強してきました。
端的に言えば、この逆のことをするのが因数分解です。例えば、$(x+2)(x-4)$を$x^2-2x-8$にするのが展開で、逆に$x^2-2x-8$を$(x+2)(x-4)$にするのが因数分解です。言葉で定義すると以下の通りです。
ある整式をいくつかの整式の積で表すこと
因数分解された式において、積を構成するそれぞれの整式
$(x+2)(x-4)$であれば、$x+2$と$x-4$の2つが因数です。「因数」の積に「分解」するから因数分解なのです。
因数分解を学ぶ意義
因数分解は整式の操作の中で最も重要であると言っても過言ではありません。というのも、因数分解された状態の式というのはその式が持つ要素がシンプルな形に分解されたとても嬉しい形なのです。特に嬉しいのは、方程式や不等式を解くときです。中学で2次方程式を学習したと思いますが、そのときに因数分解による解法を習ったはずです。$x^2+x-6=0$という方程式の解は一見すると分かりませんが、$(x+3)(x-2)=0$と因数分解されていれば解は$x=-3,\,2$であるとすぐに分かります。高校数学では解かない日はないと言ってもいいほど方程式や不等式をたくさん解かされますので、解が瞬時にわかるというのは非常に嬉しいのです。
この通りやれば怖くない!因数分解の手順
因数分解の具体的な方法を学ぶ前に、因数分解の問題を解く際の手順を挙げておきます。
- 共通因数でくくる
- 公式やたすき掛けが利用できないか確認する
- 置き換えによって公式が利用できるようになることもあるので注意
- 複2次式$ax^4+bx^2+c$のパターンに当てはまっているかを確認する
- それぞれの文字の種類ごとに次数を数え、最も次数が小さい文字1つについて降べきの順に整理する
- 係数を共通因数のくくりだしや公式・たすき掛けで因数分解する
- ここまでできたらもう一度手順1からやり直す
これを、それ以上因数分解できない形になるまで繰り返す。
因数分解の学びたてのときは個別の方法をバラバラに教えられますが、実際に因数分解をする際にはそれらを組み合わせて解いていきます。その際に、思いつきでテキトーに因数分解してしまうと時間がかかったり、できるはずの因数分解を見落としたりしてしまいます。確実に因数分解の問題を攻略するためにもこの手順は必ずマスターしてください。
ここからは、具体的にそれぞれの手順の詳細を見ていきます。なお、このページでは手順1「共通因数のくくり出し」と手順2「公式・たすき掛けの利用」について見ていきます。手順3~5については、以下のページで詳しく解説していますので、合わせて確認してください。
※記事の公開までお待ちください※
共通因数のくくりだし
共通因数のくくりだしは、分配法則$A(B+C)=AB+AC$を逆向きに活用することを基礎としています。
(1) $8x^2y^2-6xy^3$を因数分解します。
2つの項に共通して含まれるものを探します。係数の$8$と$6$はともに$2$で割り切れるので、$2$が共通因数になります。$x$については前の項が2次、後ろの項が1次なので共通して含まれるのは1つです。$y$については前の項が2次、後ろの項が3次なので共通して含まれるのは2つです。まとめると$2xy^2$が共通因数となるので、これをくくり出します。
$$\begin{align*}&\hspace{1.3em}8x^2y^2-6xy^3\\&=2xy^2\cdot 4x-2xy^2\cdot 3y\\&=2xy^2(4x-3y)\end{align*}$$
(2) $5(2x-7y)-6x^2+21xy$を因数分解します。
$5(2x-7y)$の部分ですでに$(2x-7y)$がくくられている点に注目し、後ろの2項でこの形が作れないかを考えます。すると、
$$\begin{align*}&\hspace{1.3em}-6x^2+21xy\\&=(-3x)\cdot 2x+(-3x)\cdot (-7y)\\&=-3x(2x-7y)\end{align*}$$
とくくり出すことができました。これで、$(2x-7y)$が共通因数となるので、以下のように因数分解できます。
$$\begin{align*}&\hspace{1.3em}5(2x-7y)-6x^2+21xy\\&=5(2x-7y)-3x(2x-7y)\\&=(5-3x)(2x-7y) \quad \leftarrow \textsf{ここまででも可}\\&=-(3x-5)(2x-7y)\end{align*}$$
因数分解の公式
因数分解は展開の逆の操作であると話しました。したがって、以下の展開の公式は、右辺から左辺に向かって逆向きに見ることでそのまま因数分解の公式として利用することができます。
$$\begin{align*}[\mathrm{A}]\quad&(a+b)^2=a^2+2ab+b^2\\ [\mathrm{B}]\quad&(a-b)^2=a^2-2ab+b^2\\ [\mathrm{C}]\quad&(a+b)(a-b)=a^2-b^2\\ [\mathrm{D}]\quad&(x+a)(x+b)=x^2+(a+b)x+ab\\ [\mathrm{E_1}]\quad&(ax+b)(cx+d)=acx^2+(ad+bc)x+bd\\ [\mathrm{E_2}]\quad&(ax+by)(cx+dy)=acx^2+(ad+bc)xy+bdy^2\\ [\mathrm{F}]\quad&(a+b+c)^2=a^2+b^2+c^2+2ab+2bc+2ca\\ [\mathrm{G}]\quad&(a+b)^3=a^3+3a^2b+3ab^2+b^3\\ [\mathrm{H}]\quad&(a-b)^3=a^3-3a^2b+3ab^2-b^3\\ [\mathrm{I}]\quad&(a+b)(a^2-ab+b^2)=a^3+b^3\\ [\mathrm{J}]\quad&(a-b)(a^2+ab+b^2)=a^3-b^3\\ [\mathrm{K}]\quad&(x+a)(x+b)(x+c)=x^3+(a+b+c)x^2+(ab+bc+ca)x+abc\\ [\mathrm{L}]\quad&(a+b+c)^3=a^3+b^3+c^3+3a^2b+3ab^2+3b^2c+3bc^2+3c^2a+3ca^2+6abc\\ [\mathrm{M}]\quad&(a+b+c)(a^2+b^2+c^2-ab-bc-ca)=a^3+b^3+c^3-3abc\end{align*}$$
ただし、式によって因数分解の際に頻繁に使うものもあれば、ほとんど使わないものもあります。以下では、比較的使用頻度の高いものについて具体例とともに見ていきます。
なお、もし上の展開の公式で覚えているか怪しいものがあった人は必ず下の記事で確認してから進んでください。
公式[A]・公式[B]
$$\begin{align*}[\mathrm{A}]\quad&a^2+2ab+b^2=(a+b)^2\\ [\mathrm{B}]\quad&a^2-2ab+b^2=(a-b)^2\end{align*}$$
- 項が3つの2次式(または、置き換えによって2次式にできる式)であるか
- 「なにかの2乗」である項が2つあるか
この2つに当てはまるときはこれらの公式が使えないか確かめましょう。
(1) $x^2+6xy+9y^2$を因数分解します。
項が3つの2次式であり、$x^2$は$x$の、$9y^2$は$3y$の2乗です。そこで、$2\cdot x\cdot 3y$を計算すると$6xy$となり、第2項に一致します。このことから、公式[A]が使える形であるとわかります。公式[A]の$a$に$x$を、$b$に$3y$を代入して因数分解します。
$$\begin{align*}&\hspace{1.3em}x^2+6xy+9y^2\\&=x^2+2\cdot x\cdot 3y+(3y)^2\quad \leftarrow \textsf{公式[A]の形}\\&=(x+3y)^2\end{align*}$$
(2) $(a+1)^2-10(a+1)+25$を因数分解します。
$a+1$が2箇所に出ているのでこれをひとかたまりに捉えます。$(a+1)^2$は$a+1$の、$25$は$5$の2乗なので、$2 \cdot (a+1) \cdot 5$を計算すると$10(a+1)$となり、これに$-$をつければ真ん中の形に一致します。したがって、この式には公式[B]が適用できます。
$$\begin{align*}&\hspace{1.3em}(a+1)^2-10(a+1)+25\\&=(a+1)^2-2\cdot (a+1)\cdot 5+5^2\quad \leftarrow \textsf{公式[B]の形}\\&=\{(a+1)-5\}^2\\&=(a-4)^2\end{align*}$$
わかりにくい場合は$A=a+1$と置き換えて計算してみてください。ただ、最終的には置き換えを頭の中で済ませて、紙の上では上記のように計算できるようになりましょう。
公式[C]
$$\begin{align*}[\mathrm{C}]\quad&a^2-b^2=(a+b)(a-b)\end{align*}$$
「なにかの2乗」から「なにかの2乗」を引いている場合は、この公式を使って因数分解ができます。
(1) $9x^2-49y^2$を因数分解します。
$9x^2$は$3x$の、$49y^2$は$7y$の2乗なので、公式[C]が使えます。公式[C]の$a$に$3x$を、$b$に$7y$を代入して因数分解します。
$$\begin{align*}&\hspace{1.3em}9x^2-49y^2\\&=(3x)^2-(7y)^2\quad \leftarrow \textsf{公式[C]の形}\\&=(3x+7y)(3x-7y)\end{align*}$$
(2) $a^4-4b^2+20b-25$を因数分解します。
$-4b^2+20b-25$の部分が変形できそうと予想し、次のようにしてみます。
$$\begin{align*}&\hspace{1.3em}a^4-4b^2+20b-25\\&=a^4-(4b^2-20b+25)\end{align*}$$
括弧の中に注目すると、$4b^2$は$2b$の、$25$は$5$の2乗であり、$2\cdot 2b\cdot 5=20b$が成り立つので、公式[B]が使えることがわかります。
$$\begin{align*}&\hspace{1.3em}a^4-(4b^2-20b+25)\\&=a^4-\{(2b)^2-2\cdot 2b\cdot 5+5^2\}\quad \leftarrow \textsf{公式[B]の形(中括弧内)}\\&=a^4-(2b-5)^2\end{align*}$$
後ろが2乗の形になったので、公式[C]を念頭に前の$a^4$もなにかの2乗の形に変形できないか考えると、指数法則より$a^4=a^{2\times 2}=\qty(a^2)^2$と変形できます。
公式[C]を使って因数分解すれば完成です。
$$\begin{align*}&\hspace{1.3em}a^4-4b^2+20b-25\\&=a^4-(4b^2-20b+25)\\&=\qty(a^2)^2-(2b-5)^2\quad \leftarrow \textsf{公式[C]の形}\\&=\{a^2+(2b-5)\}\{a^2-(2b-5)\}\\&=(a^2+2b-5)(a^2-2b+5)\end{align*}$$
公式[D]
$$\begin{align*}[\mathrm{D}]\quad&x^2+(a+b)x+ab=(x+a)(x+b)\end{align*}$$
2次の係数が$1$である2次式に対しては、この公式の利用を検討します。和が1次の係数、積が定数項になるような2数が見つかったときは、公式[D]を使って因数分解します。
(1) $x^2+8x-20$を因数分解します。
公式[D]が使えそうな形なので、和が$8$で積が$-20$である2数を考えます。$10$と$-2$が適するので、この2数を$a,\,b$に当てはめて公式[D]を用います。
$$\begin{align*}&\hspace{1.3em}x^2+8x-20\\&=x^2+\{10+(-2)\}x+10\cdot (-2)\quad \leftarrow \textsf{公式[D]の形}\\&=(x+10)(x-2)\end{align*}$$
(2) $x^2-px-2(p-3)(p-6)$を因数分解します。
公式[D]を利用するために、和が$-p$で積が$-2(p-3)(p-6)$である2式を考えます。積は$-1\times 2\times (p-3)\times (p-6)$という4つの要素に分解できます。これを2つに分けて和が$-p$になるようにしたいのですが、和が1次式になることに注目します。例えば、$(p-3)\times(p-6)$と$-1\times 2$という2式に分けてしまうと和は2次式になります。$p-3$と$p-6$を一緒にしている限り和が2次式になってしまうので、$p-3$と$p-6$は別の組にしておかなければなりません。すると、考えられる分け方は
$$\begin{align*}p-3\quad &\textsf{と}\quad {-1}\times 2\times (p-6)\\-1\times (p-3)\quad &\textsf{と}\quad 2\times (p-6)\\2\times (p-3)\quad &\textsf{と}\quad {-1}\times (p-6)\\-1\times 2\times (p-3)\quad &\textsf{と}\quad p-6\end{align*}$$
の4通りとなります。和が$-p$となる組は一番下なので、この2式を公式[D]に当てはめます。
$$\begin{align*}&\hspace{1.3em}x^2-px-2(p-3)(p-6)\\&=x^2+\{(-2p+6)+(p-6)\}x+(-2p+6)\cdot (p-6)\quad \leftarrow \textsf{公式[D]の形}\\&=(x-2p+6)(x+p-6)\end{align*}$$
公式[E1]・公式[E2] ~たすき掛け~
$$\begin{align*}[\mathrm{E_1}]\quad&acx^2+(ad+bc)x+bd=(ax+b)(cx+d)\\ [\mathrm{E_2}]\quad&acx^2+(ad+bc)xy+bdy^2=(ax+by)(cx+dy)\end{align*}$$
ここからは高校数学で初めて取り扱う公式です。2次式の因数分解で、2次の係数が$1$でない場合はこの公式で因数分解を行います。この公式を用いて因数分解するためには$a,\,b,\,c,\,d$の4つに当てはまる適切な数を見つけ出す必要がありますが、そのために「たすき掛け」と呼ばれる手法を用います。
① 2次の係数と定数項をそれぞれ2数の積に分解します。
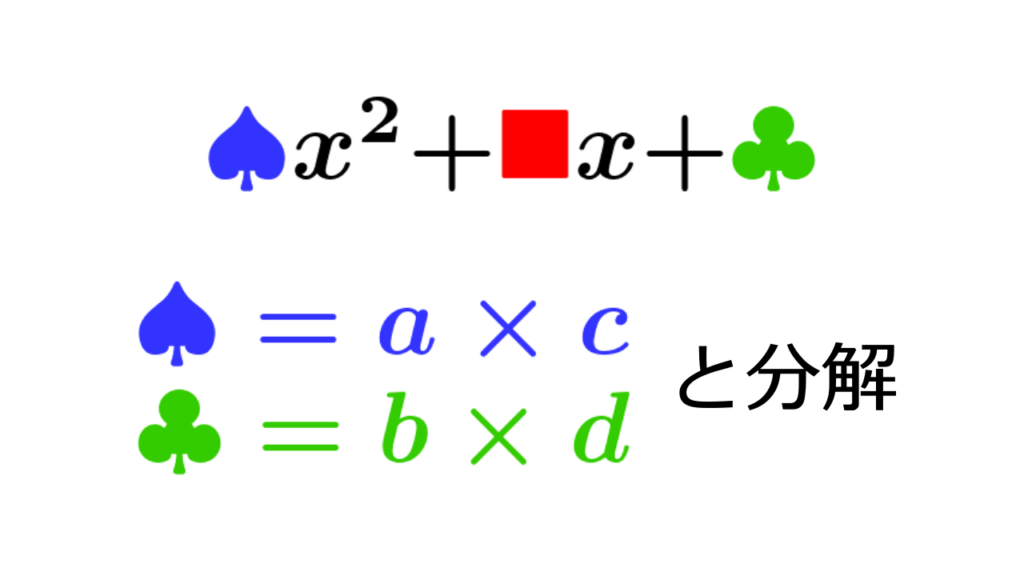
② 分解した2数それぞれを縦に並べます。

③ 斜めに配置された数どうしを掛け合わせます。
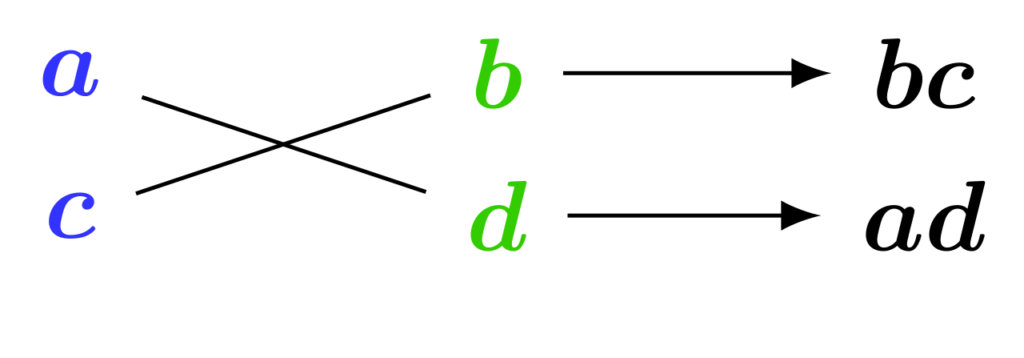
④ ③の掛け算の結果を足し合わせ、1次の係数に合致すればたすき掛け成功です。合致しなかった場合は①に戻り、別の積でたすき掛けをやり直します。
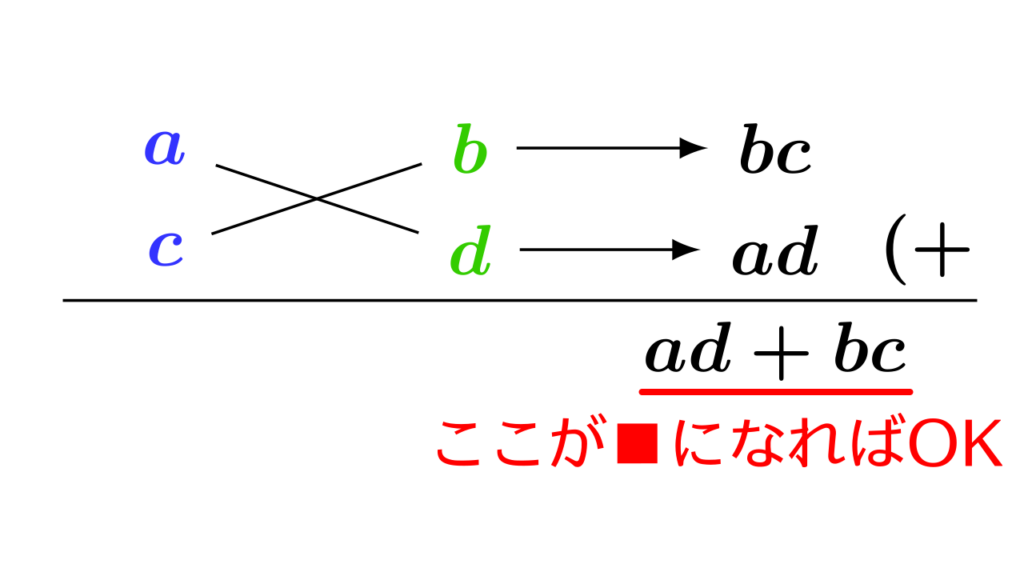
⑤ 横に並んだ数を下の図のように読み取れば、2つの因数が得られます。

たすき掛けで因数分解をする様子を具体例で見ていきましょう。
(1) $3x^2+10x+8$を因数分解します。
2次の係数が$1$でない2次式なので、公式[E1]の使用を考えます。$a,\,b,\,c,\,d$に当てはまる数を探すために、たすき掛けをします。上の手順に沿ってやってみましょう。
① 2次の係数と定数項をそれぞれ2数の積に分解します。
今回は、2次の係数を$3=1\times 3$に、定数項を$8=4\times 2$に分解してみます。
② 分解した2数それぞれを縦に並べます。

③ 斜めに配置された数どうしを掛け合わせます。
図のように、$3\times 4=12$と$1\times 2=2$になります。
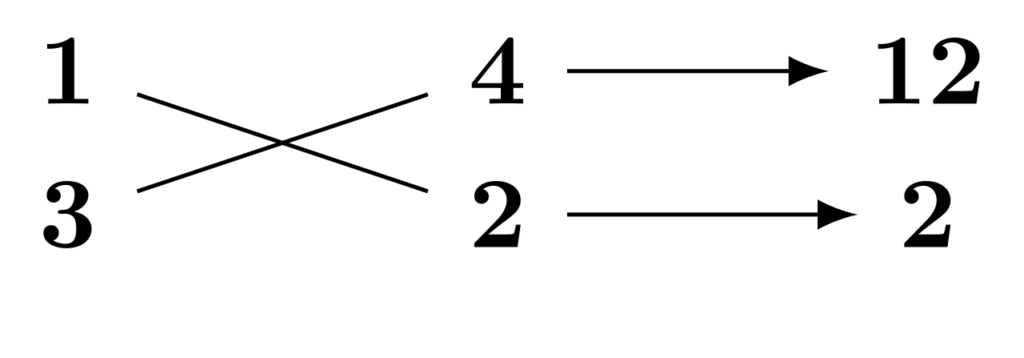
④ ③の掛け算の結果を足し合わせ、1次の係数に合致すればたすき掛け成功です。
今回は$12+2=14$となり、1次の係数は$10$なので合致しません。合致しなかった場合は①に戻り、別の積でやり直します。
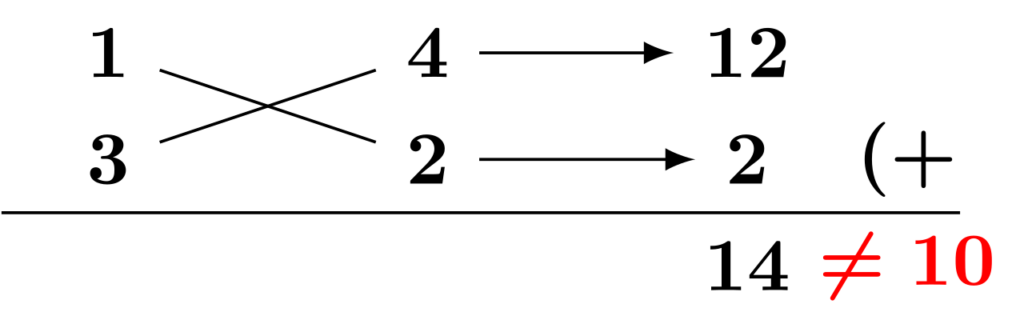
今度は$3=1\times 3,\,8=2\times 4$としてみましょう。($4$と$2$を逆にしてみました。)先程と同様にたすき掛けをしてみると、結果が$10$になってくれたので成功です。
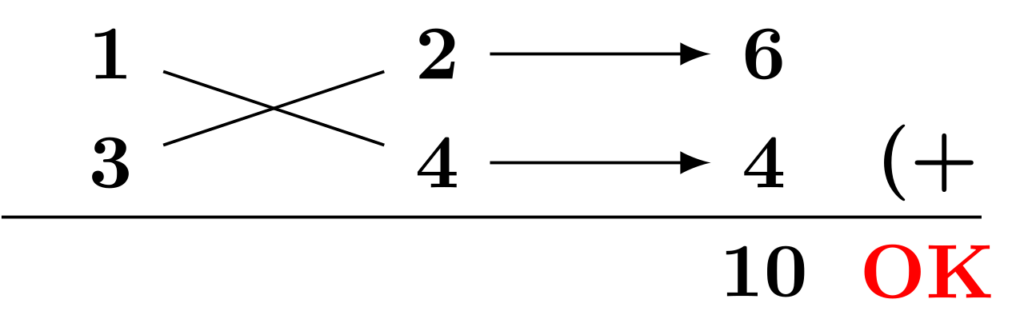
⑤ 横に並んだ数を読み取り、2つの因数を得ます。
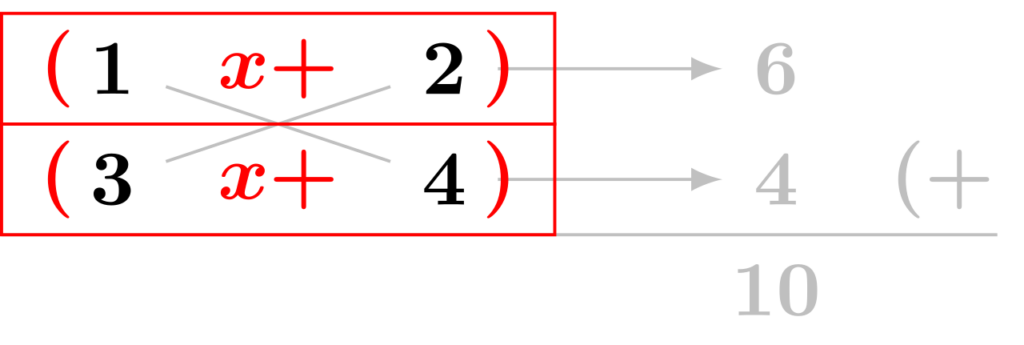
因数分解の結果は$3x^2+10x+8=(x+2)(3x+4)$となります。答えを書くときは$x$の係数が$1$の場合はルール通り省略しましょう。
(2) $6x^2-19xy+15y^2$を因数分解します。
公式[E2]が使えそうな形なので、たすき掛けで因数分解をしていきます。このとき、1次の係数が$-19$と負の数になっていることに注目します。この場合、①での積の分解を[正]×[正]のパターンばかり考えていても④での結果が正の数となり、1次の係数に合致することはありません。よって、2次の係数か定数項のどちらかを[負]×[負]に分解する必要があります。このとき、2次の係数は[正]×[正]とし、定数項を[負]×[負]に分解するのが一般的です。あとは正解の組み合わせを見つけるまで試行錯誤で計算していきましょう。
以下のように、$6=2\times 3,\,15=(-3)\times (-5)$とすると、結果が$-19$となります。
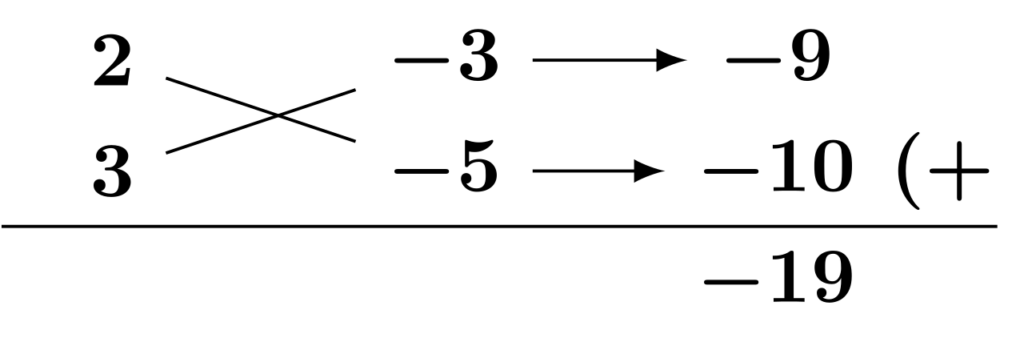
ここから因数を作りますが、注意点が2つあります。1つ目は定数項を負の数で分解したので、そのマイナスを引き継いで因数を作ります。2つ目は公式[E2]に当てはめているので、それぞれの因数の後ろの項に$y$を付けます。
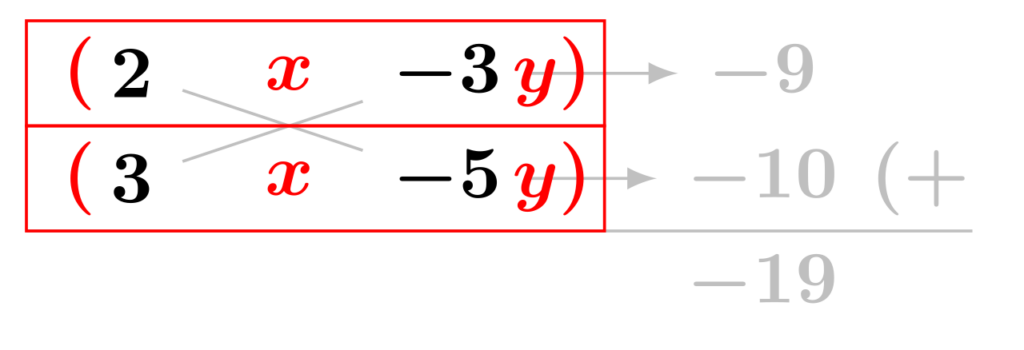
結果は$6x^2-19xy+15y^2=(2x-3y)(3x-5y)$となります。
(3) $-5a^2-a+4$を因数分解します。
公式[E1]による因数分解を考えます。コツとして、2次の係数が負のときは全体をマイナスでくくってからたすき掛けをすることで、2次の係数の積の分解を[正]×[正]のパターンだけ考えれば良くなります。今回の場合は$-5a^2-a+4=-(5a^2+a-4)$とし、括弧の中の$5a^2+a-4$に対してたすき掛けをします。
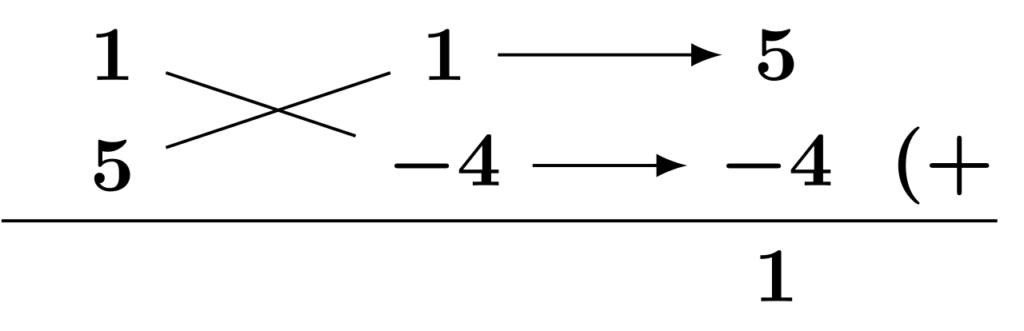
上の図より$5a^2+a-4=(a+1)(5a-4)$となるので、両辺にマイナスを掛けて$-5a^2-a+4=-(a+1)(5a-4)$となります。
(4) $2x^2-ax-(a+1)(a+2)$を因数分解します。
公式[E1]による因数分解を考えます。係数が文字式になっていますが、考え方は変わりません。
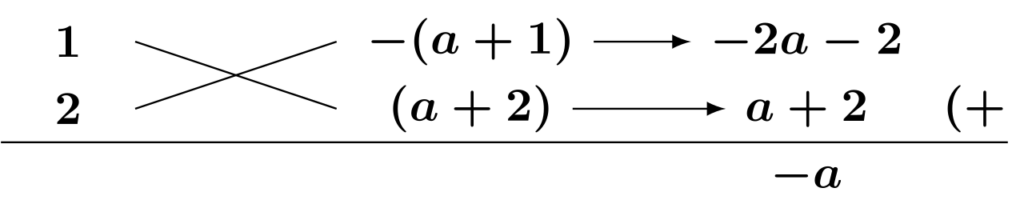
上の図より、$$\begin{align*}&\hspace{1.3em}2x^2-ax-(a+1)(a+2)\\&=\{x-(a+1)\}\{2x+(a+2)\}\\&=(x-a-1)(2x+a+2)\end{align*}$$となります。
たすき掛けの計算スピードを上げるには、問題をたくさん解いて独特の手順になれるのが一番です。自身を持てるまで何度も練習しましょう。一方で、知っておくと少し楽にたすき掛けができるポイントもいくつかあります。補足↓で説明していますので、こちらも見てください。
公式[G]・公式[H]
$$\begin{align*}[\mathrm{G}]\quad&a^3+3a^2b+3ab^2+b^3=(a+b)^3\\ [\mathrm{H}]\quad&a^3-3a^2b+3ab^2-b^3=(a-b)^3\end{align*}$$
3次式の因数分解公式です。「なにかの3乗」になっている項が2つあるときはこの公式が使える可能性があります。
(1) $x^3+9x^2+27x+27$を因数分解します。
項が4つある3次式です。$x^3$は$x$の3乗、$27$は$3$の3乗なので、公式[G]が使えそうです。$a$に$x$を、$b$に$3$を代入すると、
$$\begin{align*}&\hspace{1.3em}a^3+3a^2b+3ab^2+b^3\\&=x^3+3\cdot x^2\cdot 3 +3\cdot x\cdot 3^2+3^3\\&=x^3+9x^2+27x+27\end{align*}$$
となり、問題の式に一致します。よって、
$$x^3+9x^2+27x+27=(x+3)^3$$
と因数分解できます。
(2) $8a^3-60a^2b+150ab^2-125b^3$を因数分解します。
項が4つある3次式であり、$8a^3$は$2a$の、$125b^3$は$5b$の3乗なので、各項の符号も考慮すると公式[H]を使うことになりそうです。実際、$a$に$2a$を、$b$に$5b$を代入すると、
$$\begin{align*}&\hspace{1.3em}a^3-3a^2b+3ab^2-b^3\\&\rightarrow (2a)^3-3\cdot (2a)^2\cdot 5b +3\cdot 2a\cdot (5b)^2-(5b)^3\\&=8a^3-60a^2b+150ab^2-125b^3\end{align*}$$
となり、問題の式に一致します。よって、
$$8a^3-60a^2b+150ab^2-125b^3=(2a-5b)^3$$
と因数分解できます。
公式[I]・公式[J]
$$\begin{align*}[\mathrm{I}]\quad&a^3+b^3=(a+b)(a^2-ab+b^2)\\ [\mathrm{J}]\quad&a^3-b^3=(a-b)(a^2+ab+b^2)\end{align*}$$
この公式は、高校数学で学習する因数分解の公式の中でも最も重要な公式です。あらゆる場面で登場するので、「3乗+3乗」や「3乗-3乗」の形を見たら因数分解できることに即座に気付けるようになりましょう。
(1) $27x^3+1$を因数分解します。
$27x^3$は$3x$の3乗、$1$は$1$の3乗なので、「3乗+3乗」の形になっています。よって、公式[I]を使って因数分解できます。
$$\begin{align*}&\hspace{1.3em}27x^3+1\\&=(3x)^3+1^3\quad \leftarrow \textsf{公式[I]の形}\\&=(3x+1)\{(3x)^2-3x\cdot 1+1^2\}\\&=(3x+1)(9x^2-3x+1)\end{align*}$$
(2) $p^6-8q^3$を因数分解します。
指数法則より$p^6=p^{2\times 3}=\qty(p^2)^3$なので、$p^6$は$p^2$の3乗です。
$8q^3$は$2q$の3乗なので、「3乗-3乗」の形になっています。よって、公式[J]を使って因数分解できます。
$$\begin{align*}&\hspace{1.3em}p^6-8q^3\\&=\qty(p^2)^3-(2q)^3\quad \leftarrow \textsf{公式[J]の形}\\&=(p^2-2q)\qty{\qty(p^2)^2+p^2 \cdot 2q+(2q)^2}\\&=(p^2-2q)(p^4+2p^2q+4q^2)\end{align*}$$
公式[M]
$$\begin{align*}[\mathrm{M}]\quad&a^3+b^3+c^3-3abc=(a+b+c)(a^2+b^2+c^2-ab-bc-ca)\end{align*}$$
3乗が3つ登場するときは、この公式を使って因数分解できる可能性があります。以下の例の(2)のように、一見するとこの公式が使えるとはわからない形で出題されることもあるので要注意です。
(1) $8x^3+27y^3-z^3+18xyz$を因数分解します。
$8x^3$は$2x$の、$27y^3$は$3y$の、$-z^3$は$-z$の3乗なので、公式[M]が使えそうです。公式[M]の左辺の$a$に$2x$を、$b$に$3y$を、$c$に$-z$を代入すると、
$$\begin{align*}&\hspace{1.3em}a^3+b^3+c^3-3abc\\&=(2x)^3+(3y)^3+(-z)^3-3\cdot 2x\cdot 3y\cdot (-z)\\&=8x^3+27y^3-z^3+18xyz\end{align*}$$
となり、問題の式に一致します。よって、公式[M]を用いて
$$\begin{align*}&\hspace{1.3em}8x^3+27y^3-z^3+18xyz\\&=(2x)^3+(3y)^3+(-z)^3-3\cdot 2x\cdot 3y\cdot (-z)\quad \leftarrow \textsf{公式[M]の形}\\&=\{2x+3y+(-z)\}\{(2x)^2+(3y)^2+(-z)^2-2x\cdot 3y-3y\cdot (-z)-(-z)\cdot 2x\}\\&=(2x+3y-z)(4x^2+9y^2+z^2-6xy+3yz+2zx)\end{align*}$$
と因数分解できます。
(2) $x^3-3xy+y^3+1$を因数分解します。
$x^3$は$x$の、$y^3$は$y$の、$1$は$1$の3乗になっています。公式とは項の並び順が違いますが、公式[M]が使えそうな形だと気付かなかければなりません。$a$に$x$を、$b$に$y$を、$c$に$1$を代入すると、
$$\begin{align*}&\hspace{1.3em}a^3+b^3+c^3-3abc\\&=x^3+y^3+1^3-3\cdot x\cdot y\cdot 1\\&=x^3+y^3+1-3xy\end{align*}$$
となり、問題の式に一致します。公式[M]を用いると、
$$\begin{align*}&\hspace{1.3em}x^3-3xy+y^3+1\\&=x^3+y^3+1^3-3\cdot x\cdot y\cdot 1\quad \leftarrow \textsf{公式[M]の形}\\&=(x+y+1)(x^2+y^2+1^2-x\cdot y-y\cdot 1-1\cdot x)\\&=(x+y+1)(x^2+y^2+1-xy-y-x)\\&=(x+y+1)(x^2-xy+y^2-x-y+1)\end{align*}$$
と因数分解できます。解答を書くときは、降べきの順に並べるように意識しましょう。
さて、この公式[M]にはもう一つ、よりハイレベルな因数分解公式があります。公式[M]
$$a^3+b^3+c^3-3abc=(a+b+c)(a^2+b^2+c^2-ab-bc-ca)$$
において、$a+b+c=0$が成り立っているとしましょう。すると、右辺にこれを代入すると
$$a^3+b^3+c^3-3abc=0\times (a^2+b^2+c^2-ab-bc-ca)$$
すなわち、
$$a^3+b^3+c^3-3abc=0$$
となります。$-3abc$を右辺に移項すると
$$a^3+b^3+c^3=3abc$$
となりました。右辺の$3abc$は積の形なので、この等式は$a+b+c=0$が成り立つときだけ使える特殊な因数分解公式ということができます。
$$\begin{align*}[\mathrm{M’}]\quad&a+b+c=0\,\textsf{のとき}\quad a^3+b^3+c^3=3abc\end{align*}$$
和が$0$になる3つのものがそれぞれ3乗されて足し合わされているときは、この公式を使って因数分解できます。この公式$\textsf{[M’]}$は暗記を前提とされることはあまりなく、先に公式[M]を証明させてから出題したり、
$$\begin{align*}&\textsf{等式}\;a^3+b^3+c^3=(a+b+c)(a^2+b^2+c^2-ab-bc-ca)+3abc\\ &\textsf{を用いて次の式を因数分解せよ。}\end{align*}$$
といった誘導がつくことが多いです。ですが、せっかくなのでこの記事を見ている皆さんはこのパターンも誘導なしに解けるようになってしまいましょう。
$(x-y)^3+(y-z)^3+(z-x)^3$を因数分解します。
与えられた式は$x-y,\,y-z,\,z-x$という3つの式の3乗の和となっています。この3つの式を足し合わせると、
$$(x-y)+(y-z)+(z-x)=0$$
となるので、公式$\textsf{[M’]}$が利用できます。$a$に$x-y$を、$b$に$y-z$を、$c$に$z-x$を代入して、
$$(x-y)^3+(y-z)^3+(z-x)^3=3(x-y)(y-z)(z-x)$$
となります。
公式まとめ
詳しく解説しなかったものも含め、すべての公式をまとめておきます。
$$\begin{align*}[\mathrm{A}]\quad&a^2+2ab+b^2=(a+b)^2\\ [\mathrm{B}]\quad&a^2-2ab+b^2=(a-b)^2\\ [\mathrm{C}]\quad&a^2-b^2=(a+b)(a-b)\\ [\mathrm{D}]\quad&x^2+(a+b)x+ab=(x+a)(x+b)\\ [\mathrm{E_1}]\quad&acx^2+(ad+bc)x+bd=(ax+b)(cx+d)\quad\leftarrow\textsf{たすき掛けの利用}\\ [\mathrm{E_2}]\quad&acx^2+(ad+bc)xy+bdy^2=(ax+by)(cx+dy)\quad\leftarrow\textsf{たすき掛けの利用}\\ [\mathrm{G}]\quad&a^3+3a^2b+3ab^2+b^3=(a+b)^3\\ [\mathrm{H}]\quad&a^3-3a^2b+3ab^2-b^3=(a-b)^3\\ [\mathrm{I}]\quad&a^3+b^3=(a+b)(a^2-ab+b^2)\\ [\mathrm{J}]\quad&a^3-b^3=(a-b)(a^2+ab+b^2)\\ [\mathrm{M}]\quad&a^3+b^3+c^3-3abc=(a+b+c)(a^2+b^2+c^2-ab-bc-ca)\\ [\mathrm{M’}]\quad&a+b+c=0\,\textsf{のとき}\quad a^3+b^3+c^3=3abc\end{align*}$$
以下の公式は、因数分解においてはほとんど使わない。
$$\begin{align*}[\mathrm{F}]\quad&a^2+b^2+c^2+2ab+2bc+2ca=(a+b+c)^2\\ [\mathrm{K}]\quad&x^3+(a+b+c)x^2+(ab+bc+ca)x+abc=(x+a)(x+b)(x+c)\\ [\mathrm{L}]\quad&a^3+b^3+c^3+3a^2b+3ab^2+3b^2c+3bc^2+3c^2a+3ca^2+6abc=(a+b+c)^3\end{align*}$$
複数回の変形が必要な因数分解
因数分解を行う際には、それ以上分解できない形まで変形を行うのが原則です。そのために、複数回の因数分解が必要な場合も多いです。その際には、こちらで説明した因数分解の手順に従って順番に行いましょう。
(1) $12a^3b+60a^2b^2+63ab^3$を因数分解します。
初めに、共通因数を探します。係数を確認すると$12,\,60,\,63$はいずれも$3$の倍数なので、$3$でくくることができます。また、文字に注目するといずれの項も$a$と$b$を1個は含んでいるので、$ab$でくくることができます。
$$12a^3b+60a^2b^2+63ab^3=3ab(4a^2+20ab+21b^2)$$
くくられた後の括弧の中の式$4a^2+20ab+21b^2$がさらに因数分解できないか考えます。共通因数でくくったばかりでこれ以上共通因数について考えるのは無駄なので、公式やたすき掛けの使用について検討すると、たすき掛けを使うことができそうな2次式だとわかります。実際、以下のようにたすき掛けができます。
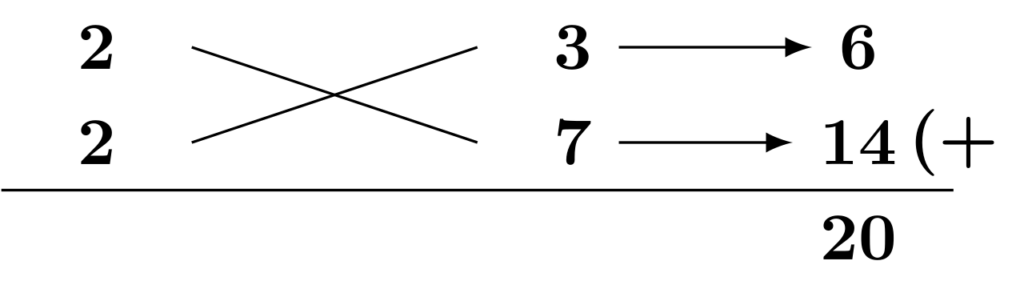
したがって、
$$\begin{align*}&\hspace{1.3em}12a^3b+60a^2b^2+63ab^3\\&=3ab(4a^2+20ab+21b^2) \qquad\textsf{(共通因数のくくりだし)}\\&=3ab(2a+3b)(2a+7b)\qquad\textsf{(公式[E2]の利用・たすき掛け)}\end{align*} $$
となります。
(2) $x^3+2x^2-9x-18$を因数分解します。
すべての項に共通する因数はありませんが、一部の項だけの組み合わせでくくり出すことで共通因数を作り出すことができます。
前2項と後ろ2項に分けてみましょう。前2項は$x^3+2x^2=x^2(x+2)$とくくることができます。後ろ2項は$-9x-18=-9(x+2)$とくくることができるので、$x+2$が共通因数となります。$x+2$をくくり出すと「2乗-2乗」の形が出てくるので公式[C]で変形します。
$$\begin{align*}&\hspace{1.3em}x^3+2x^2-9x-18\\&=x^2(x+2)-9(x+2)\\&=(x+2)(x^2-9)\qquad\textsf{(共通因数のくくりだし)}\\&=(x+2)(x+3)(x-3)\qquad\textsf{(公式[C]の利用)}\end{align*}$$
組み合わせを変えても因数分解できる場合があります。
$$\begin{align*}&\hspace{1.3em}x^3+2x^2-9x-18\\&=(x^3-9x)+(2x^2-18)\\&=x(x^2-9)+2(x^2-9)\\&=(x^2-9)(x+2)\qquad\textsf{(共通因数のくくりだし)}\\&=(x+3)(x-3)(x+2)\qquad\textsf{(公式[C]の利用)}\end{align*}$$
(3) $p^6-64$を因数分解します。
$p^6$を$p^3$の、$64$を$8$の2乗と見て「2乗-2乗」の公式[C]で因数分解する方法と、$p^6$を$p^2$の、$64$を$4$の3乗と見て「3乗-3乗」の公式[J]で因数分解する方法が考えられます。
公式[C]を使って因数分解すると以下のようになります。
$$\begin{align*}&\hspace{1.3em}p^6-64\\&=\qty(p^3)^2-8^2\\&=(p^3+8)(p^3-8)\end{align*}$$
$p^3+8,\,p^3-8$はそれぞれ「3乗+3乗」、「3乗-3乗」の形になっているので、公式[I]および公式[J]で因数分解できます。
$$\begin{align*}&\hspace{1.3em}p^6-64\\&=(p^3+8)(p^3-8)\qquad\textsf{(公式[C]の利用)}\\&=(p+2)(p^2-2p+4)(p-2)(p^2+2p+4)\qquad\textsf{(公式[I]・公式[J]の利用)}\\&=(p-2)(p+2)(p^2-2p+4)(p^2+2p+4)\qquad\textsf{(次数が小さい因数を前へ)}\end{align*}$$
最初に公式[J]を使うと以下のようになります。
$$\begin{align*}&\hspace{1.3em}p^6-64\\&=\qty(p^2)^3-4^3\\&=(p^2-4)(p^4+4p^2+16)\end{align*}$$
$p^2-4$は「2乗-2乗」の形なので公式[C]が使えます。$p^4+4p^2+16$は共通因数のくくり出しや公式が使えない少し難しい形です。複2次式の因数分解のテクニックを使うと因数分解できます。複2次式の因数分解については以下の記事を見てください。
※記事の公開までお待ちください※
結果は以下のようになります。
$$\begin{align*}&\hspace{1.3em}p^6-64\\&=(p^2-4)(p^4+4p^2+16)\qquad\textsf{(公式[J]の利用)}\\&=(p+2)(p-2)(p^4+8p^2+16-4p^2)\qquad\textsf{(公式[C]の利用・複2次式パターンの準備)}\\&=(p+2)(p-2)\qty{(p^2+4)^2-(2p)^2}\qquad\textsf{(公式[A]で複2次式の形に)}\\&=(p+2)(p-2)(p^2+4+2p)(p^2+4-2p)\qquad\textsf{(公式[C]の利用)}\\&=(p-2)(p+2)(p^2-2p+4)(p^2+2p+4)\qquad\textsf{(降べきの順に整理)}\end{align*}$$
どちらの方法でも因数分解ができましたが、公式[C]から始めるほうが簡単に因数分解できました。これは、公式[C]の分解後の式がもう一度公式に当てはめやすい形だからです。
練習問題
ここまでに学習した因数分解の方法について確認しましょう。因数分解の手順は、まず共通因数のくくり出し、次に公式の利用です。公式を使うことだけに頭がいっぱいにならないように気をつけましょう。
問題
次の式を因数分解せよ。$$\begin{align*}(1)\quad&8a^3bc^2-12a^2b^3c+20abc^4\\(2)\quad&20y^2-15xy+(7x+2y)(3x-4y)\\(3)\quad&x^2-\frac{\,4\,}{9}\\(4)\quad&p^2+p-56\\(5)\quad&8p^2-26pq-7q^2\\(6)\quad&6x^2+37xy+6y^2\\(7)\quad&36x^2+93x+60\\(8)\quad&18x^2-39x+20\\(9)\quad&8x^3-24x^2+18x\\(10)\quad&64a^3-48a^2+12a-1\\(11)\quad&4x^3-16x^2-9x+36\\(12)\quad&8x^4y+27xy^7\\(13)\quad&a^3-64b^3-8c^3-24abc\\(14)\quad&x^9-1\\(15)\quad&4(x-3)^2+36(x-3)+81\\(16)\quad&x^2-(a+11)x-6a^2+13a+28\\(17)\quad&3y^2+(4x+1)y+x^2-3x-10\\(18)\quad&6a^2-(b+4)a-5(b+1)(3b+2)\\(19)\quad&a^2-b^2-9c^2-6bc+4a+4\\(20)\quad&(x+y-2z)^3+(y+z-2x)^3+(z+x-2y)^3\end{align*}$$
解説
(1) まずは、共通因数をくくり出します。係数は$8,\,-12,\,20$といずれも$4$の倍数なので、$4$でくくることができます。また、$a$については前の項から順に3次、2次、1次なので1つくくり出せます。$b$や$c$についても同様に調べると1つずつくくり出せることがわかります。
$$\begin{align*}&\hspace{1.3em}8a^3bc^2-12a^2b^3c+20abc^4\\&=4abc(2a^2c-3ab^2+5c^3)\qquad\textsf{(共通因数のくくり出し)}\end{align*}$$
ここからさらなる因数分解が可能かを考えますが、この式はこれ以上因数分解できない状態なのでこれが解答となります。(公式の形に当てはめることができないのを確認してください。)
(2) 後ろの部分がすでに積の形になっているので、前の2項で$7x+2y$か$3x-4y$のいずれかを作り出せて共通因数としてくくる事ができるかもしれないと予想しましょう。この予想をもとに前の2項に注目すると、$5y$でくくり出せることがわかります。
$$\begin{align*}&\hspace{1.3em}20y^2-15xy+(7x+2y)(3x-4y)\\&=5y(4y-3x)+(7x+2y)(3x-4y)\end{align*}$$
すると、$4y-3x$という形が出現します。これは$3x-4y$の符号を入れ替えたものになっています。よって、マイナスを出すことで共通因数$3x-4y$を作り出すことができます。
$$\begin{align*}&\hspace{1.3em}20y^2-15xy+(7x+2y)(3x-4y)\\&=5y(4y-3x)+(7x+2y)(3x-4y)\\&=-5y(3x-4y)+(7x+2y)(3x-4y)\\&=(3x-4y)\{-5y+(7x+2y)\}\qquad\textsf{(共通因数のくくり出し)}\\&=(3x-4y)(7x-3y)\end{align*}$$
(3) 初めに共通因数がないかを確認しますが、今回は共通因数はありません。(以降、共通因数がない場合は共通因数についての記述を省きますが、皆さんは必ず初めに共通因数の有無を確認してください。)次に、公式が使えるかを検討します。$\dfrac{\,4\,}{9}$は$\dfrac{\,2\,}{3}$の2乗なので、公式[C]の形になっています。
$$\begin{align*}&\hspace{1.3em}x^2-\frac{\,4\,}{9}\\&=\left(x+\frac{2}{3}\right)\left(x-\frac{\,2\,}{3}\right)\qquad\textsf{(公式[C]の利用)}\end{align*}$$
係数に分数が含まれる場合、以下のように分数を前に出してから因数分解する方法もあります。
$$\begin{align*}&\hspace{1.3em}x^2-\frac{\,4\,}{9}\\&=\frac{1}{\,9\,}(9x^2-4)\\&=\frac{1}{\,9\,}(3x+2)(3x-2)\qquad\textsf{(公式[C]の利用)}\end{align*}$$
因数分解の公式[C]
$$a^2-b^2=(a+b)(a-b)$$
(4) 2次式で2次の係数が$1$なので、公式[D]が使えるかもしれないと考えましょう。公式[D]を使うためには「足して$1$、掛けて$-56$」となる2数を見つける必要があります。そのような2数として$8$と$-7$が見つかるので、これを用いて公式[D]で因数分解します。
$$\begin{align*}&\hspace{1.3em}p^2+p-56\\&=(p+8)(p-7)\qquad\textsf{(公式[D]の利用)}\end{align*}$$
因数分解の公式[D]
$$x^2+(a+b)x+ab=(x+a)(x+b)$$
(5) 2次の係数が$1$でない2次式なので、たすき掛けができないかを考えます。今回は、以下のようにたすき掛けができるので、これに従って公式[E2]で因数分解します。
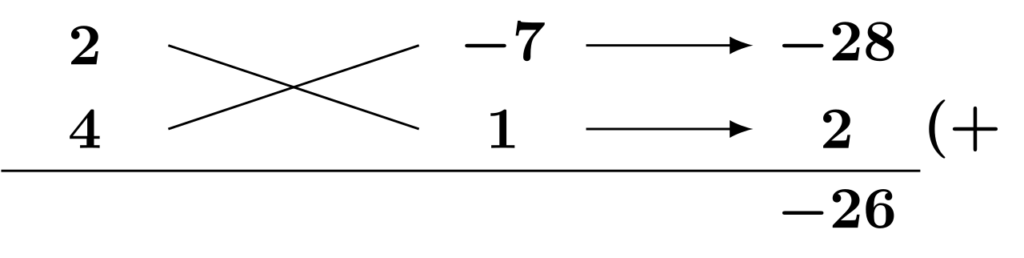
$$\begin{align*}&\hspace{1.3em}8p^2-26pq-7q^2\\&=(2p-7q)(4p+q)\qquad\textsf{(公式[E2]の利用・たすき掛け)}\end{align*}$$
因数分解の公式[E2]
$$acx^2+(ad+bc)xy+bdy^2=(ax+by)(cx+dy)$$
(6) こちらも2次の係数が$1$でない2次式なので、たすき掛けを検討します。
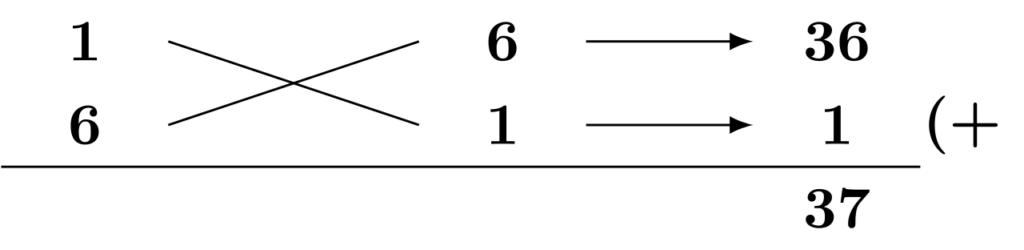
$$\begin{align*}&\hspace{1.3em}6x^2+37xy+6y^2\\&=(x+6y)(6x+y)\qquad\textsf{(公式[E2]の利用・たすき掛け)}\end{align*}$$
因数分解の公式[E2]
$$acx^2+(ad+bc)xy+bdy^2=(ax+by)(cx+dy)$$
(7) この問題は共通因数があります。全ての係数が$3$で割れるので、$3$でくくりましょう。
$$\begin{align*}&\hspace{1.3em}36x^2+93x+60\\&=3(12x^2+31x+20)\end{align*}$$
括弧内の式がさらに因数分解ができないかを考えると、たすき掛けができます。
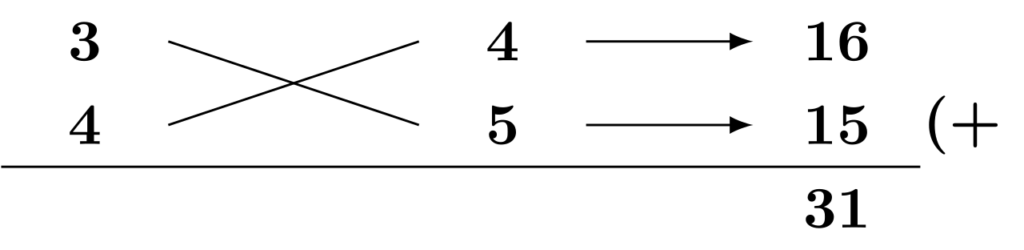
以上をまとめると、次のようになります。
$$\begin{align*}&\hspace{1.3em}36x^2+93x+60\\&=3(12x^2+31x+20)\qquad\textsf{(共通因数のくくり出し)}\\&=3(3x+4)(4x+5)\qquad\textsf{(公式[E1]の利用・たすき掛け)}\end{align*}$$
因数分解の公式[E1]
$$acx^2+(ad+bc)x+bd=(ax+b)(cx+d)$$
(8) こちらもたすき掛けで因数分解します。
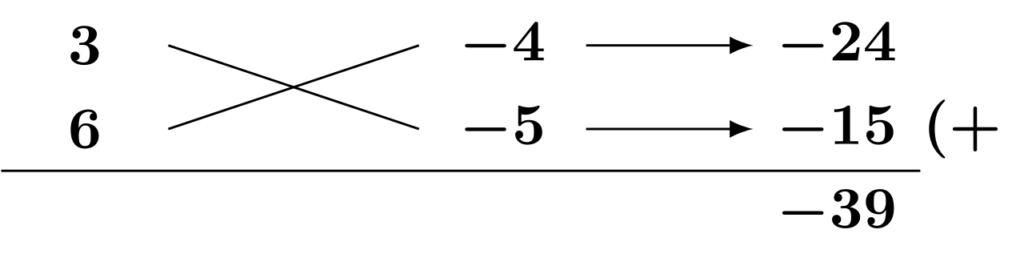
$$\begin{align*}&\hspace{1.3em}18x^2-39x+20\\&=(3x-4)(6x-5)\qquad\textsf{(公式[E1]の利用・たすき掛け)}\end{align*}$$
因数分解の公式[E1]
$$acx^2+(ad+bc)x+bd=(ax+b)(cx+d)$$
(9) まずは共通因数$2x$でくくりましょう。
$$\begin{align*}&\hspace{1.3em}8x^3-24x^2+18x\\&=2x(4x^2-12x+9)\end{align*}$$
括弧内の式に注目します。$4x^2$は$2x$の2乗、$9$は$3$の2乗であり、$12x=2\cdot 2x\cdot 3$なので、公式[B]の形になっています。
$$\begin{align*}&\hspace{1.3em}8x^3-24x^2+18x\\&=2x(4x^2-12x+9)\qquad\textsf{(共通因数のくくり出し)}\\&=2x(2x-3)^2\qquad\textsf{(公式[B]の利用)}\end{align*}$$
因数分解の公式[B]
$$a^2-2ab+b^2=(a-b)^2$$
(10) $64a^3$は$4a$の3乗、$1$は$1$の3乗なので、公式[H]が使えそうな形です。公式[H]の左辺の$a$に$4a$を、$b$に$1$を当てはめると、
$$\begin{align*}&\hspace{1.3em}a^3-3a^2b+3ab^2-b^3\\&\rightarrow (4a)^3-3\cdot (4a)^2\cdot 1 +3\cdot 4a\cdot (1)^2-(1)^3\\&=64a^3-48a^2+12a-1\end{align*}$$
となり、問題の式に一致します。よって、
$$\begin{align*}&\hspace{1.3em}64a^3-48a^2+12a-1\\&=(4a-1)^3\qquad\textsf{(公式[H]の利用)}\end{align*}$$
因数分解の公式[H]
$$a^3-3a^2b+3ab^2-b^3=(a-b)^3$$
(11) 一見すると、公式[G]や公式[H]を使いたくなる形ですが、うまく当てはめることができません。また、すべての項に共通する因数はありません。しかし、前の2項と後ろの2項に分けると、それぞれで共通因数があります。
$$\begin{align*}&\hspace{1.3em}4x^3-16x^2-9x+36\\&=(4x^3-16x^2)-(9x-36)\\&=4x^2(x-4)-9(x-4)\end{align*}$$
それぞれの共通因数でくくると、$x-4$が共通して出てきますので、これをくくり出します。
$$\begin{align*}&\hspace{1.3em}4x^2(x-4)-9(x-4)\\&=(x-4)(4x^2-9)\end{align*}$$
すると、$4x^2-9$は公式[C]でさらに因数分解できます。まとめると、次のようになります。
$$\begin{align*}&\hspace{1.3em}4x^3-16x^2-9x+36\\&=(4x^3-16x^2)-(9x-36)\qquad\textsf{(前2項と後ろ2項に分ける)}\\&=4x^2(x-4)-9(x-4)\qquad\textsf{(それぞれの共通因数でくくり出し)}\\&=(x-4)(4x^2-9)\qquad\textsf{(共通因数のくくり出し)}\\&=(x-4)(2x+3)(2x-3)\qquad\textsf{(公式[C]の利用)}\end{align*}$$
なお、以下のように因数分解することもできます。
$$\begin{align*}&\hspace{1.3em}4x^3-16x^2-9x+36\\&=(4x^3-9x)-(16x^2-36)\qquad\textsf{(第1・3項と第2・4項に分ける)}\\&=x(4x^2-9)-4(4x^2-9)\qquad\textsf{(それぞれの共通因数でくくり出し)}\\&=(x-4)(4x^2-9)\qquad\textsf{(共通因数のくくり出し)}\\&=(x-4)(2x+3)(2x-3)\qquad\textsf{(公式[C]の利用)}\end{align*}$$
因数分解の公式[C]
$$a^2-b^2=(a+b)(a-b)$$
(12) まずは共通因数のくくり出しです。$xy$が共通因数なのでくくり出します。
$$\begin{align*}&\hspace{1.3em}8x^4y+27xy^7\\&=xy(8x^3+27y^6)\end{align*}$$
すると、$8x^3$は$2x$の3乗、$27y^6$は$3y^2$の3乗なので、公式[I]を当てはめることができます。
$$\begin{align*}&\hspace{1.3em}8x^4y+27xy^7\\&=xy(8x^3+27y^6)\qquad\textsf{(共通因数のくくり出し)}\\&=xy(2x+3y^2)\qty{\qty(2x)^2-2x\cdot 3y^2+\qty(3y^2)^2}\qquad\textsf{(公式[I]の利用)}\\&=xy(2x+3y^2)(4x^2-6xy^2+9y^4)\end{align*}$$
因数分解の公式[I]
$$a^3+b^3=(a+b)(a^2-ab+b^2)$$
(13) 問題の式が公式[M]に近い形をしていることに気付きましょう。実際、公式[M]の$a$を$a$に、$b$を$-4b$に、$c$を$-2c$に置き換えると、
$$\begin{align*}&\hspace{1.3em}a^3+b^3+c^3-3abc\\&=a^3+(-4b)^3+(-2c)^3-3\cdot (-4b)\cdot (-2c)\\&=a^3-64b^3-8c^3-24abc\end{align*}$$
となり、問題の式に一致します。
$$\begin{align*}&\hspace{1.3em}a^3-64b^3-8c^3-24abc\\&=\{a+(-4b)+(-2c)\}\{a^2+(-4b)^2+(-2c)^2-a\cdot (-4b)-(-4b)\cdot (-2c)-(-2c)\cdot a\}\qquad\textsf{(公式[M]の利用)}\\&=(a-4b-2c)(a^2+16b^2+4c^2+4ab-8bc+2ca)\end{align*}$$
因数分解の公式[M]
$$a^3+b^3+c^3-3abc=(a+b+c)(a^2+b^2+c^2-ab-bc-ca)$$
(14) 因数分解をするには公式を使うしかなさそうな短い式です。式の形から、使える公式は[C]か[J]のどちらかしかなさそうです。$1$は$1$の2乗とも3乗ともみなせるので、$x^9$がなにかの2乗になるなら公式[C]、なにかの3乗になるなら公式[J]を使うことになります。指数法則より、$x^9=x^{3\times 3}=\qty(x^3)^3$なので、$x^9$は$x^3$の3乗です。よって、公式[J]で因数分解できます。
$$\begin{align*}&\hspace{1.3em}x^9-1\\&=(x^3)^3-1\\&=(x^3-1)\{(x^3)^2+x^3\cdot 1+1^2\}\\&=(x^3-1)(x^6+x^3+1)\end{align*}$$
ここで安心してはいけません。$x^3-1$は公式[J]でもう一度因数分解できます。
$$\begin{align*}&\hspace{1.3em}x^9-1\\&=(x^3)^3-1\\&=(x^3-1)\qty{\qty(x^3)^2+x^3\cdot 1+1^2}\qquad\textsf{(公式[J]の利用)}\\&=(x^3-1)(x^6+x^3+1)\\&=(x-1)(x^2+x+1)(x^6+x^3+1)\qquad\textsf{(公式[J]の利用)}\end{align*}$$
因数分解の公式[J]
$$a^3-b^3=(a-b)(a^2+ab+b^2)$$
(15) 式中に$x-3$が繰り返し登場するので、これらは展開せずひとかたまりと見ます。つまり、頭の中では$4X^2+36X+81$という式の因数分解だと考えます。$4X^2$は$2X$の2乗、$81$は$9$の2乗であり、$36X=2\cdot 2X\cdot 9$なので、公式[A]が使えます。$X$には$x-3$が当てはまることに注意して因数分解しましょう。
$$\begin{align*}&\hspace{1.3em}4(x-3)^2+36(x-3)+81\\&\textcolor[rgb]{0.25,0.5,1}{\hspace{0.3em}=4X^2+36X+81\qquad\textsf{(}X=x-3\,\textsf{と置き換え)}}\\&\textcolor[rgb]{0.25,0.5,1}{\hspace{0.3em}=(2X+9)^2}\\&=\{2(x-3)+9\}^2\qquad\textsf{(公式[A]の利用)}\\&=(2x+3)^2\\&\hspace{2em}\textcolor[rgb]{0.25,0.5,1}{\textsf{※青字部分は頭の中で処理!}}\end{align*}$$
因数分解の公式[A]
$$a^2+2ab+b^2=(a+b)^2$$
(16) $-6a^2+13a+28$の部分がたすき掛けで因数分解できそうです。実際、以下のように因数分解できます。
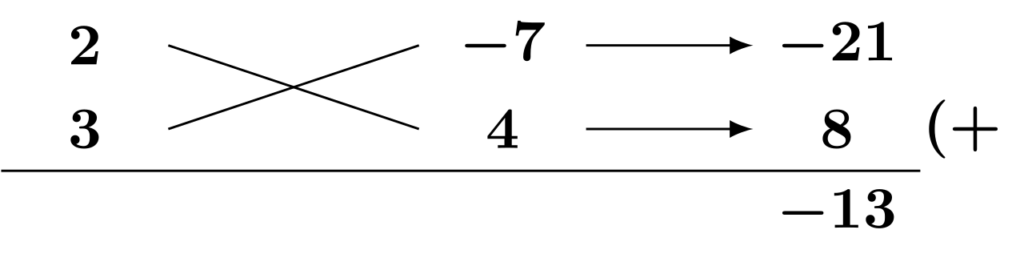
$$\begin{align*}&\hspace{1.3em}-6a^2+13a+28\\&=-(6a^2-13a-28)\\&=-(2a-7)(3a+4)\qquad\textsf{(公式[E1]の利用・たすき掛け)}\end{align*}$$
これにより、式全体はこのようになります。
$$\begin{align*}&\hspace{1.3em}x^2-(a+11)x-6a^2+13a+28\\&=x^2-(a+11)x-(2a-7)(3a+4)\end{align*}$$
これは、$x$の2次式であり2次の係数が$1$なので、公式[D]の形と考えることができます。和が$-(a+11)$で積が$-(2a-7)(3a+4)$となる2式を考えると、$2a-7$と$-(3a+4)$の組が見つかります。
$$\begin{align*}&\hspace{1.3em}x^2-(a+11)x-6a^2+13a+28\\&=x^2-(a+11)x-(2a-7)(3a+4)\\&=\{x+(2a-7)\}\{x-(3a+4)\}\qquad\textsf{(公式[D]の利用)}\\&=(x+2a-7)(x-3a-4)\end{align*}$$
因数分解の公式[E1]
$$acx^2+(ad+bc)x+bd=(ax+b)(cx+d)$$
因数分解の公式[D]
$$x^2+(a+b)x+ab=(x+a)(x+b)$$
(17) $x^2-3x-10$を公式[D]で因数分解すると、
$$\begin{align*}&\hspace{1.3em}x^2-3x-10\\&=(x-5)(x+2)\qquad\textsf{(公式[D]の利用)}\end{align*}$$
となります。よって、式全体は
$$\begin{align*}&\hspace{1.3em}3y^2+(4x+1)y+x^2-3x-10\\&=3y^2+(4x+1)y+(x-5)(x+2)\end{align*}$$
となり、2次の係数が$1$でない$y$の2次式なので、たすき掛けでの因数分解ができそうと予想します。実際にたすき掛けを行うと、以下のように因数分解ができます。
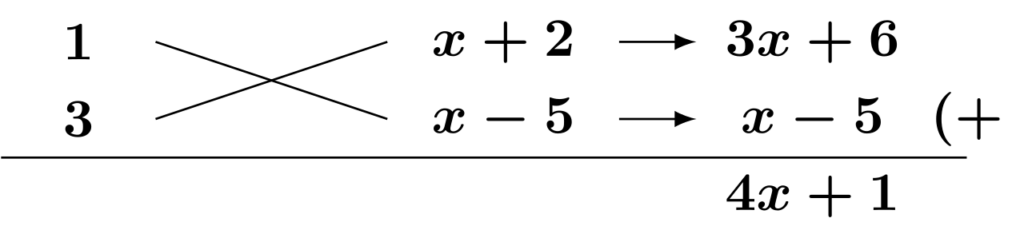
$$\begin{align*}&\hspace{1.3em}3y^2+(4x+1)y+x^2-3x-10\\&=3y^2+(4x+1)y+(x-5)(x+2)\\&=\{y+(x+2)\}\{3y+(x-5)\}\qquad\textsf{(公式[E1]の利用・たすき掛け)}\\&=(x+y+2)(x+3y-5)\end{align*}$$
因数分解の公式[D]
$$x^2+(a+b)x+ab=(x+a)(x+b)$$
因数分解の公式[E1]
$$acx^2+(ad+bc)x+bd=(ax+b)(cx+d)$$
(18) 係数が文字式のたすき掛けです。積の組み合わせの可能性が多いので、根気強く計算して試していきましょう。先に$b$の係数だけに注目して合致するかどうか計算して、一致したときだけ定数項も計算するようにすると、労力を減らせます。
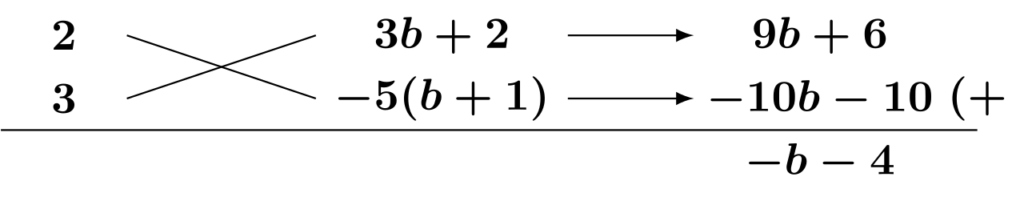
$$\begin{align*}&\hspace{1.3em}6a^2-(b+4)a-5(b+1)(3b+2)\\&=\{2a+(3b+2)\}\{3a-5(b+1)\}\qquad\textsf{(公式[E1]の利用・たすき掛け)}\\&=(2a+3b+2)(3a-5b-5)\end{align*}$$
因数分解の公式[E1]
$$acx^2+(ad+bc)x+bd=(ax+b)(cx+d)$$
(19) 共通因数を持たず、公式にも当てはめられない形です。(一見すると公式[F]に近いですが、問題の式に一致させるように$a,\,b,\,c$を置き換えることができません。)この式を因数分解するには、$a$だけが登場する項と$b,\,c$が登場する項に分離できることに気づかないといけません。
$$\begin{align*}&\hspace{1.3em}a^2-b^2-9c^2-6bc+4a+4\\&=(a^2+4a)+(-b^2-6bc-9c^2)+4\end{align*}$$
ここで、$b$と$c$が登場する項に注目すると、
$$\begin{align*}&\hspace{1.3em}-b^2-6bc-9c^2\\&=-(b^2+6bc+9c^2)\\&=-(b+3c)^2\qquad\textsf{(公式[A]の利用)}\end{align*}$$
と変形できることがわかります。そして、残された項に注目すると、
$$\begin{align*}&\hspace{1.3em}a^2+4a+4\\&=(a+2)^2\qquad\textsf{(公式[A]の利用)}\end{align*}$$
この変形により、公式[C]が使えるようになります。
$$\begin{align*}&\hspace{1.3em}a^2-b^2-9c^2-6bc+4a+4\\&=(a^2+4a+4)+(-b^2-6bc-9c^2)\\&=(a+2)^2-(b+3c)^2\\&=\{(a+2)+(b+3c)\}\{(a+2)-(b+3c)\}\qquad\textsf{(公式[C]の利用)}\\&=(a+b+3c+2)(a-b-3c+2)\end{align*}$$
初見では難しかったかもしれません。複数種類の文字が登場する式では、文字の種類ごとに項を分離することができないか考えてみると解答の糸口がつかめることがあります。
因数分解の公式[A]
$$a^2+2ab+b^2=(a+b)^2$$
因数分解の公式[C]
$$a^2-b^2=(a+b)(a-b)$$
(20) 3乗されている3つの式を足してみると、
$$(x+y-2z)+(y+z-2x)+(z+x-2y)=0$$
となります。足すと$0$になる3つの式の3乗和の因数分解は公式$\textsf{[M’]}$の出番です。気付けましたか?
$$\begin{align*}&\hspace{1.3em}(x+y-2z)^3+(y+z-2x)^3+(z+x-2y)^3\\&=3(x+y-2z)(y+z-2x)(z+x-2y)\qquad\textsf{(公式[M’]の利用)}\end{align*}$$
因数分解の公式$\textsf{[M’]}$
$$a+b+c=0\,\textsf{のとき}\quad a^3+b^3+c^3=3abc$$
公式$\textsf{[M’]}$が使えることに気づかなかった場合でも、以下のようにして因数分解をすることができます。かなり重厚な計算ですが、練習にはもってこいでしょう。
$$\begin{align*}&\hspace{1.3em}(x+y-2z)^3+(y+z-2x)^3+(z+x-2y)^3\\&\qquad\textsf{↓ 前側の2つの括弧に公式[I]を適用}\\&=\{(x+y-2z)+(y+z-2x)\}\{(x+y-2z)^2-(x+y-2z)(y+z-2x)+(y+z-2x)^2\}+(z+x-2y)^3\\&\qquad\textsf{↓ 前の中括弧を整理 後ろの中括弧は展開すると大変なのでそのままおいておく}\\&=(-x+2y-z)\{(x+y-2z)^2-(x+y-2z)(y+z-2x)+(y+z-2x)^2\}+(z+x-2y)^3\\&\qquad\textsf{↓ 1つ目の小括弧からマイナスを出して前後を入れ替え}\\&=(z+x-2y)^3-(z+x-2y)\{(x+y-2z)^2-(x+y-2z)(y+z-2x)+(y+z-2x)^2\}\\&\qquad\textsf{↓ 共通因数のくくり出し}\\&=(z+x-2y)[(z+x-2y)^2-\{(x+y-2z)^2-(x+y-2z)(y+z-2x)+(y+z-2x)^2\}]\\&\qquad\textsf{↓ 大括弧内 マイナスを分配}\\&=(z+x-2y)\{(z+x-2y)^2-(x+y-2z)^2+(x+y-2z)(y+z-2x)-(y+z-2x)^2\}\\&\qquad\textsf{↓ 中括弧内 前2つの括弧には公式[C]を適用 後ろ2つの括弧は共通因数のくくり出し}\\&=(z+x-2y)[\{(z+x-2y)+(x+y-2z)\}\{(z+x-2y)-(x+y-2z)\}+(y+z-2x)\{(x+y-2z)-(y+z-2x)\}]\\&\qquad\textsf{↓ 足し引きを整理}\\&=(z+x-2y)\{(2x-y-z)(3z-3y)+(y+z-2x)(3x-3z)\}\\&\qquad\textsf{↓ 中括弧内 1つ目の括弧からマイナスを出して前後入れ替え}\\&=(z+x-2y)\{(y+z-2x)(3x-3z)-(y+z-2x)(3z-3y)\}\\&\qquad\textsf{↓ 共通因数のくくり出し}\\&=(z+x-2y)(y+z-2x)\{(3x-3z)-(3z-3y)\}\\&\qquad\textsf{↓ 中括弧内を整理}\\&=(z+x-2y)(y+z-2x)(3x+3y-6z)\\&\qquad\textsf{↓ 3でくくって順番を整理}\\&=3(x+y-2z)(y+z-2x)(z+x-2y)\end{align*}$$
因数分解の公式[I]
$$a^3+b^3=(a+b)(a^2-ab+b^2)$$
因数分解の公式[C]
$$a^2-b^2=(a+b)(a-b)$$
解答
$$\begin{align*}(1)\quad&4abc(2a^2c-3ab^2+5c^3)\\(2)\quad&(3x-4y)(7x-3y)\\(3)\quad&\left(x+\frac{2}{3}\right)\left(x-\frac{\,2\,}{3}\right)\quad\textsf{または}\quad\frac{1}{\,9\,}(3x+2)(3x-2)\\(4)\quad&(p+8)(p-7)\\(5)\quad&(2p-7q)(4p+q)\\(6)\quad&(x+6y)(6x+y)\\(7)\quad&3(3x+4)(4x+5)\\(8)\quad&(3x-4)(6x-5)\\(9)\quad&2x(2x-3)^2\\(10)\quad&(4a-1)^3\\(11)\quad&(x-4)(2x+3)(2x-3)\\(12)\quad&xy(2x+3y^2)(4x^2-6xy^2+9y^4)\\(13)\quad&(a-4b-2c)(a^2+16b^2+4c^2+4ab-8bc+2ca)\\(14)\quad&(x-1)(x^2+x+1)(x^6+x^3+1)\\(15)\quad&(2x+3)^2\\(16)\quad&(x+2a-7)(x-3a-4)\\(17)\quad&(x+y+2)(x+3y-5)\\(18)\quad&(2a+3b+2)(3a-5b-5)\\(19)\quad&(a+b+3c+2)(a-b-3c+2)\\(20)\quad&3(x+y-2z)(y+z-2x)(z+x-2y)\end{align*}$$
補足
知っておくと少し楽になる たすき掛けのコツ
この先の高校数学の学習において、たすき掛けをしなければならない場面に幾度となく遭遇します。そのため、たすき掛けを素早く完了させることは高校数学において重要なスキルです。計算速度を上げる一番の方法は、たくさんの問題を何度も繰り返し解くことですが、がむしゃらにたすき掛けしているだけでは計算速度に限界があります。たすき掛けをするときに意識することで少し早く計算できるコツをいくつか紹介します。(本文中で触れたものもあります。)
2次の係数を正にして (正)×(正)に分解せよ
例として、$-6x^2+29x-20$の因数分解を考えましょう。今、2次の係数は$-6$ですが、全体をマイナスでくくって$-(6x^2-29x+20)$とすることで、2次の係数を正の数$6$にします。積が$6$となる2数の組み合わせには以下のものがあります。
$$\begin{gather}1\times 6,\, 2\times 3,\, 3\times 2,\, 6\times 1,\\(-1)\times(-6),\,(-2)\times(-3),\,(-3)\times(-2),\,(-6)\times(-1)\end{gather}$$
実は、これらの組み合わせのうち、(負)×(負)のものについては考える必要がありません。
なぜでしょうか。例えば、2次の係数を$(-1)\times(-6)$と分解し、定数項を$4\times 5$と分解した場合、たすき掛けの計算は以下の通りになります。
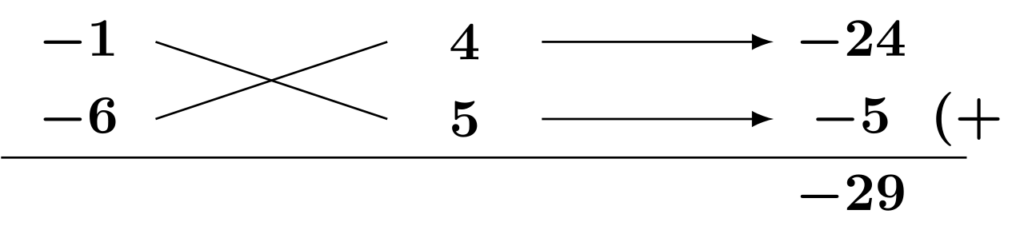
ここで、2次の係数と定数項の分解した数をそれぞれ$-1$倍してみましょう。つまり、2次の係数を$1\times 6$に、定数項を$(-4)\times (-5)$に分解します。
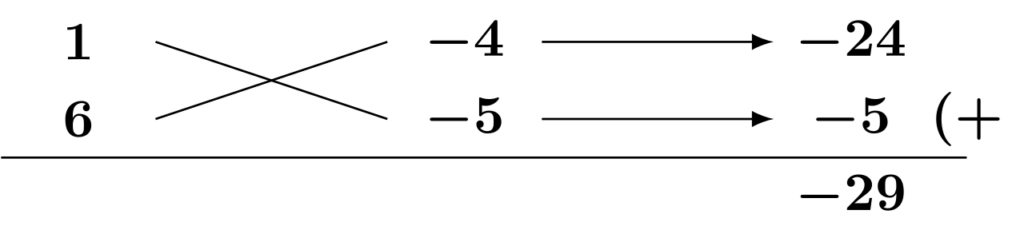
いずれもたすき掛けの結果が$-29$になりました。このように、(負)×(負)のそれぞれの組み合わせに対して、分解した数字をそれぞれ$-1$倍することでたすき掛けの結果が同じになるような(正)×(正)の組み合わせが存在します。因数分解された式の状態で見ても、
$$\begin{align*}&\hspace{1.3em}(-x+4)(-6x+5)\\&=\{(-1)\cdot(x-4)\}\{(-1)\cdot(6x-5)\}\\&=(-1)^2(x-4)(6x-5)\\&=(x-4)(6x-5)\end{align*}$$
というように、2つは全く同じであることがわかります。よって、(負)×(負)の組と(正)×(正)の組のうちいずれか一方だけを考えればよく、それならば計算が簡単な(正)×(正)だけを考えればよいということになるのです。これにより、考えるべき組み合わせは
$$\begin{gather}1\times 6,\, 2\times 3,\, 3\times 2,\, 6\times 1\end{gather}$$
だけでよくなります。正の数の積だけを考えればよいので、楽に分解できるようになります。
「分解した数字をそれぞれ$-1$倍することでたすき掛けの結果が同じになるような組み合わせが存在する」という話自体は2次の係数が負であっても成り立ちます。例えば、$(-1)\times 6$と$1\times (-6)$などが挙げられます。したがって、「積の組み合わせを減らすこと」は2次の係数を正に直さずともできるので、このことは2次の係数を正にするメリットではありません。
2次の係数を正にするメリットは「常に(正)×(正)の分解だけ考えていればよい」という状態に持ち込んで、余計な思考リソースを省くことです。計算に負の数が入り込むと思っている以上に労力がかかるので、それを無くそうという狙いです。
2次の係数の分解は 配置の上下と数の大小を固定せよ
2次の係数の積の組み合わせを更に減らすために、上下のどちらに大きいほうの数を置くのか統一するようにしましょう。
このサイトでは上に小さいほうの数、下に大きいほうの数を置くことにしています。その逆の組み合わせは考える必要はありません。なぜなら、以下のように定数項側の数字も含めて上下をごっそり入れ替えれば同じ結果になるからです。
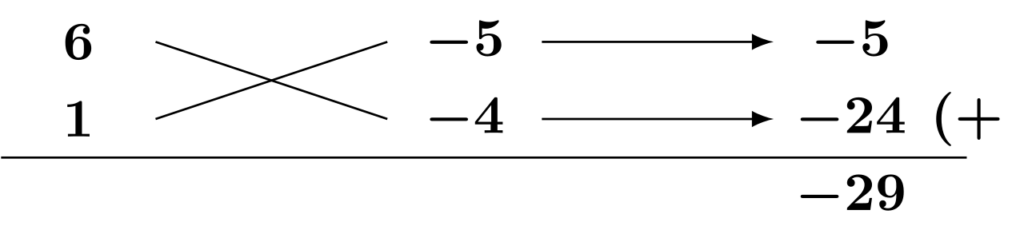

なお、2次の係数の上下を固定した場合は定数項の上下は固定できません。でなければ、全パターンのたすき掛けを網羅できないからです。
定数項もまずは(正)×(正)に分解せよ
2次の係数の分解は(正)×(正)のパターンだけ考えれば十分ですが、定数項の分解は(正)×(正)、(正)×(負)、(負)×(負)のすべての場合が考えられます。しかし、計算過程においてはまずは(正)×(正)だけを考え、後から符号を決定することで効率よくたすき掛けを決定できます。具体例で見ていきましょう。
(1) $3x^2-13x+14$を因数分解します。
2次の係数の分解方法は$1\times 3$しかありません。定数項の分解方法はいろいろ考えられますが、まずは$1\times 14$を試してみます。
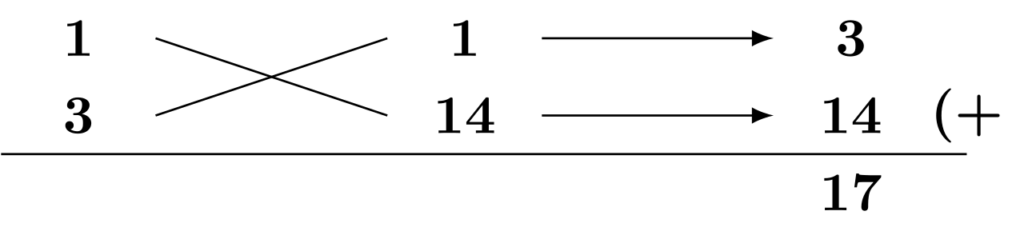
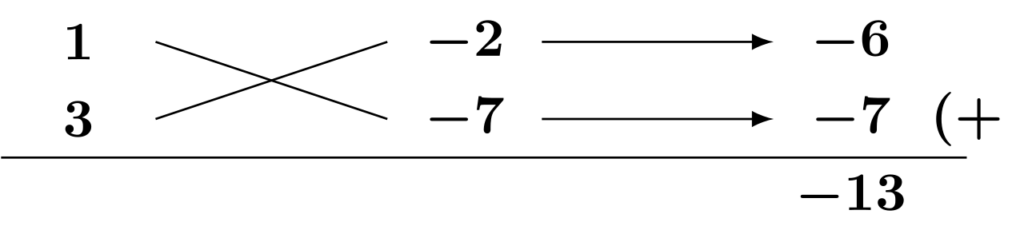
1次の係数は$-13$ですから、たすき掛けは失敗しています。ここで注目したいのが、絶対値も合致していない点です。絶対値が合致していない点から、この時点で$(-1)\times (-14)$のパターンは試す必要がありません。実際に計算すると、
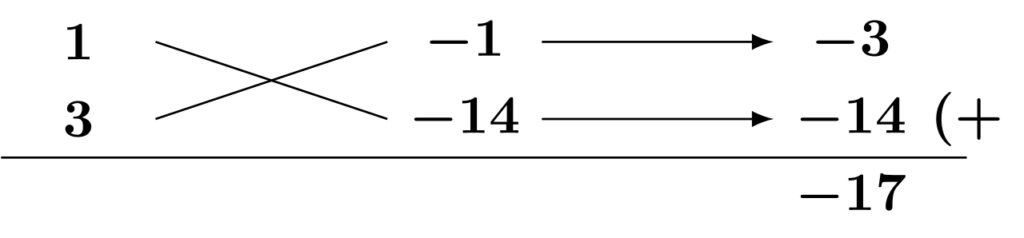
このようになり、先程の結果に$-1$倍されたものとなります。つまり、(正)×(正)で試して絶対値が一致しなかった組み合わせは、同じ絶対値の(負)×(負)の組み合わせも成功しないのです。
今度は、定数項の分解を$2\times 7$としてみましょう。
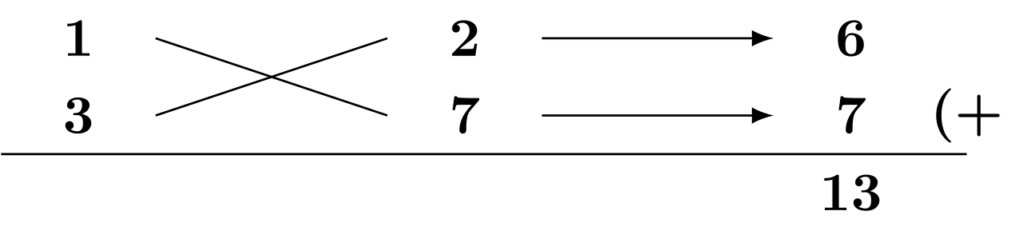
今度は1次の係数$-13$と絶対値だけが合致しました。このような場合には、定数項の分解した数字をそれぞれ$-1$倍することで、たすき掛けが成功します。
$$3x^2-13x+14=(x-2)(3x-7)$$
整理すると、以下のようになります。
[定数項が正のとき]
2次の係数と定数項をそれぞれ(正)×(正)に分解
① たすき掛けが成功 → 結果を答える
② たすき掛けの結果が絶対値だけ一致 → 定数項を同じ絶対値の(負)×(負)に変える
③ たすき掛けの結果が絶対値も一致しない → 別の(正)×(正)の組み合わせを考える
(2) $5x^2+4x-12$を因数分解します。
2次の係数は$1\times 5$と分解するしかありません。定数項は$-12$と負の数なので、本来は(正)×(負)に分解しなければいけませんが、一旦、絶対値の$12$のみに注目してこれを(正)×(正)に分解します。まずは$1\times 12$としてみましょう。
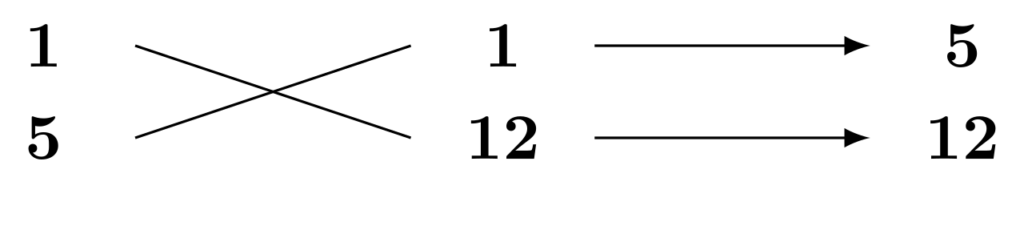
途中の斜めに掛け算をするところまで行いました。さて、実際には定数項は$(-1)\times 12$か$1\times (-12)$のどちらかに分解されます。前者の場合、右上がりの掛け算の結果が$-5$に変わるので、たすき掛けの結果は$7$になります。後者の場合、右下がりの掛け算の結果が$-12$に変わるので、たすき掛けの結果は$-7$になります。いずれにしても、たすき掛けの結果の絶対値は$7$になり、これは斜めの掛け算の2つの結果の差になります。一方、1次の係数は$4$であり、絶対値が違います。よって、上図の組み合わせでは$(-1)\times 12$にしても$1\times (-12)$にしてもたすき掛けが失敗することがわかります。このように、斜めに掛け算した2つの積の差が1次の係数の絶対値と異なる場合、その組み合わせによるたすき掛けは成功しません。
次に、定数項の分解を$2\times 6$としてみます。
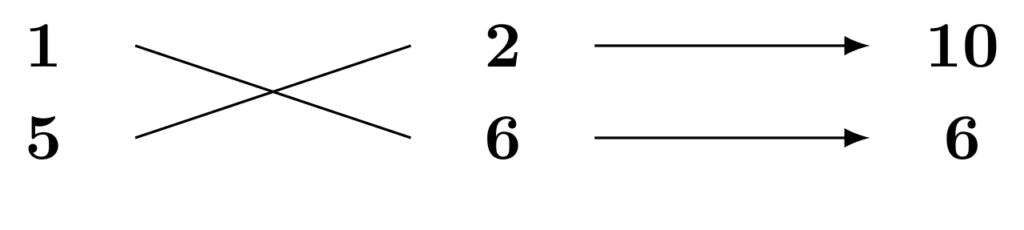
斜めの掛け算の結果の差が$4$になり、1次の係数の絶対値に一致しました。この場合、定数項を分解した2つの数字のどちらかを負に変えることでたすき掛けが完了します。今回の場合、斜めの積のうち$6$が$-6$になれば、たすき掛けの結果が$4$となるので、その状況を作るために定数項を$2\times (-6)$と分解します。
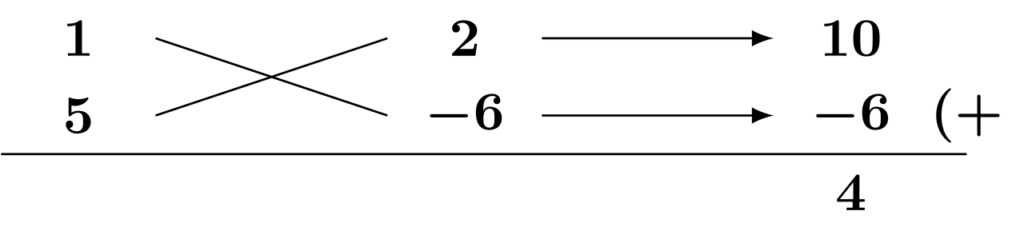
$$5x^2+4x-12=(x+2)(5x-6)$$
整理すると、以下のようになります。
[定数項が負のとき]
2次の係数と定数項の絶対値をそれぞれ(正)×(正)に分解 → 斜めの積まで計算
① 2つの積の差が1次の係数の絶対値に一致
→ 定数項を分解した2つの数のうち適切な方を負に変える
② 2つの積の差が1次の係数の絶対値に一致しない → 別の組み合わせを考える
横並びの数が同じ数の倍数なら 計算不要でその組み合わせは除外
分解した数字を並べたとき、横に並んだ数字が同じ数の倍数になっている場合、斜めの掛け算をする前にたすき掛けが成功しないことを察知できます。
$6x^2+29x+28$の因数分解で、2次の係数と定数項を以下のように分解したとします。
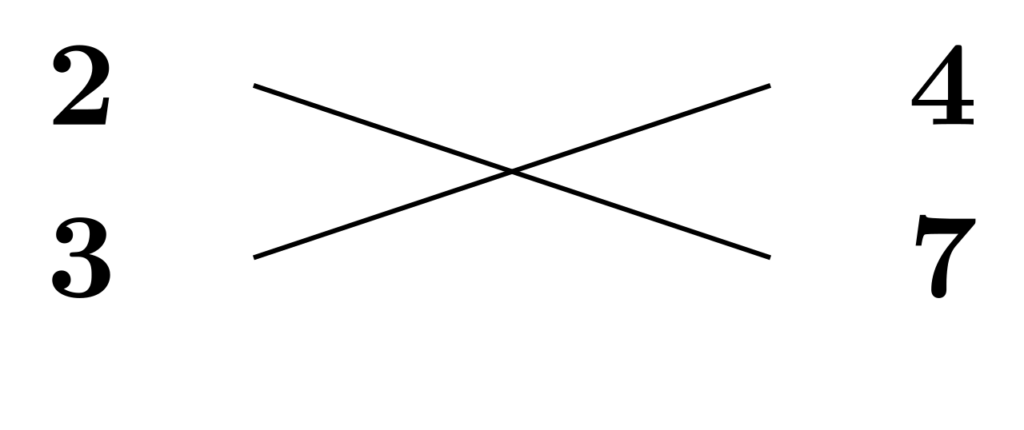
実は、このたすき掛けはこれ以上計算を進めずとも失敗することがわかってしまいます。
もし、上のたすき掛けが正しいたすき掛けだった場合、以下のように因数分解できます。
$$6x^2+29x+28=(2x+4)(3x+7)$$
ここで、$2x+4$という因数に注目するとこれは$2$をくくり出すことができます。よって、以下のように書くことができるはずです。
$$6x^2+29x+28=2(x+2)(3x+7)$$
この式の右辺に注目すると、$(x+2)(3x+7)$は展開すると2次式になり、それに$2$を掛けるので、すべて展開した後の2次式は2次の係数、1次の係数、定数項がすべて$2$の倍数になっている、すなわち、全体を$2$でくくることができるはずです。しかし、元の式$6x^2+29x+28$は全体を$2$でくくることができません。等しいと考えていたはずの2つの式が、片方は$2$でくくることができるのに、もう一方は$2$でくくることができないのは矛盾していておかしいですね。よって、この等式は間違っている、すなわち、たすき掛けは失敗していることがわかります。
このようなことになったのは、$2x+4$という$2$でくくることができる因数ができてしまったためです。そして、それは上のたすき掛けの図で、上の段にともに$2$の倍数である$2$と$4$が並んでしまったためです。
このように、共通因数でそれ以上くくれない2次式をたすき掛けで因数分解するとき、上下のどちらかの段に並ぶ2つの数が$2$以上の同じ数の倍数になっている(互いに素でない)とき、その組み合わせによるたすき掛けは成功しません。よって、このような組み合わせは斜めの積を計算する前に除外することが可能です。
係数の素因数に注目して 組み合わせを絞り込め
係数の素因数がどのように配置されるかを考えることによって、考えるべき組み合わせを大きく減らせることがあります。係数が大きい数のときに強力です。
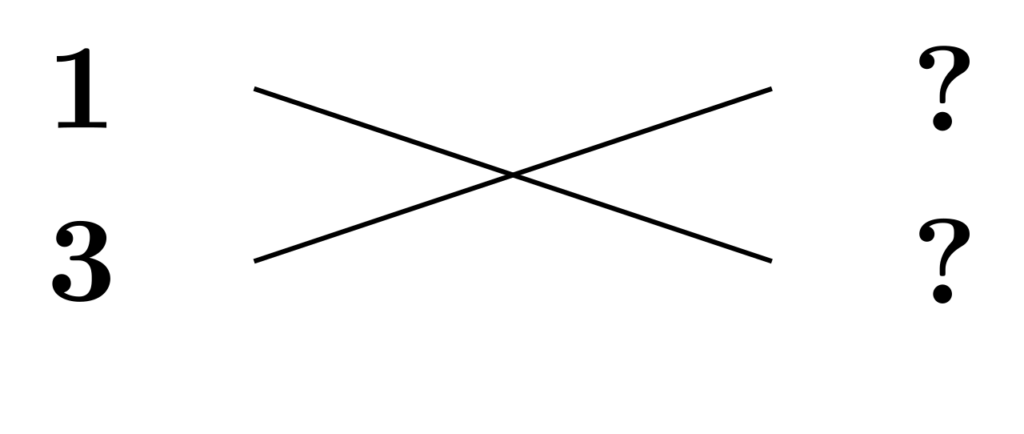
(1) $3x^2-20x+12$を因数分解します。
2次の係数は$1\times 3$以外に分解できないので、$1$を上に、$3$を下に配置します。
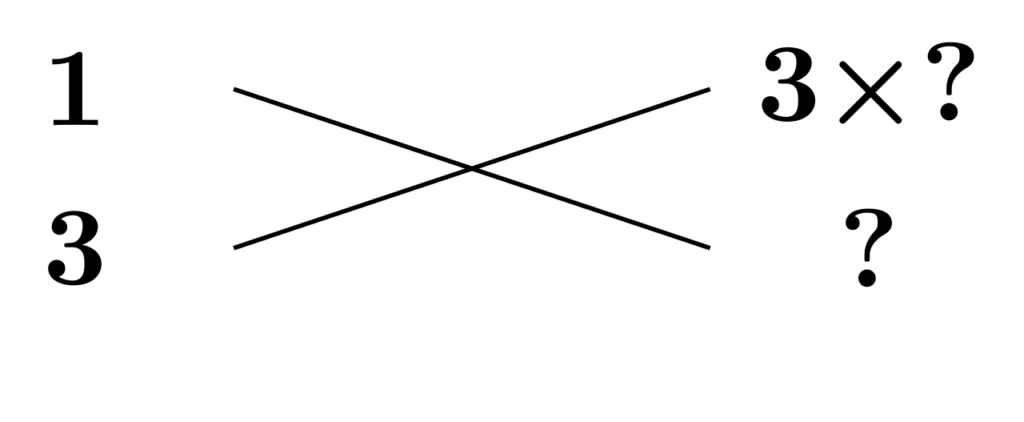
定数項の$12$は素因数分解すると$2^2\times 3$となり、素因数は全部で3つあります。定数項を2つの数の積に分解することは、この3つの素因数を上下のどちらに配置するかをそれぞれ決めることに他なりません。
まず、素因数$3$に注目します。もし、これを下に置くと、下の数字は$3$の倍数になります。すると、下段の2つの数はどちらも$3$の倍数となり、これは前項の「横並びの数は同じ数の倍数にならない」というのに反します。よって、素因数$3$は上段に置かなければなりません。
残った2つの素因数$2$について考えます。ここで、和や積の偶奇性について確認します。
(奇数)+(奇数)=(偶数)
(奇数)+(偶数)=(奇数)
(偶数)+(偶数)=(偶数)
(奇数)×(奇数)=(奇数)
(奇数)×(偶数)=(偶数)
(偶数)×(偶数)=(偶数)
これを踏まえて、例えば、定数項を(偶数)×(奇数)に分解するとどうなるでしょうか。
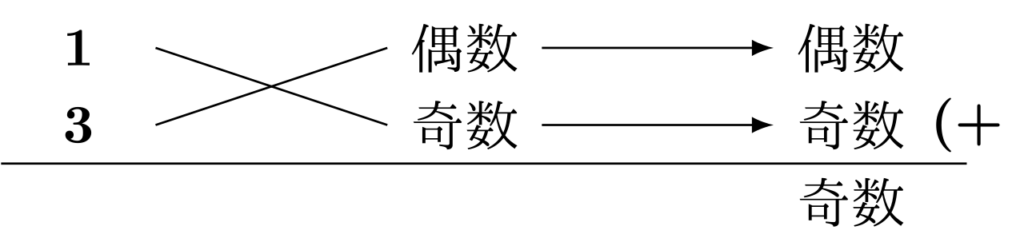
上のように、結果は奇数になります。しかし、1次の係数は$-20$で偶数です。したがって、これはありえません。
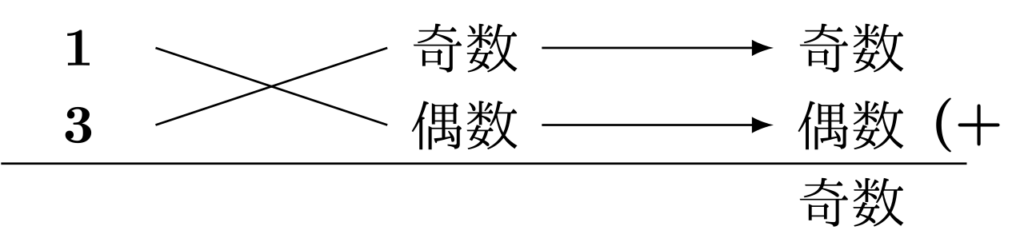
上のように、(奇数)×(偶数)と分解してみても結果が奇数になります。定数項$12$は偶数ですから、(奇数)×(奇数)と分解することはできません。よって、定数項は(偶数)×(偶数)に分解されます。偶数にするためには素因数$2$が1つは必要なので、残っていた2つの素因数$2$は上下に1つずつ配置します。
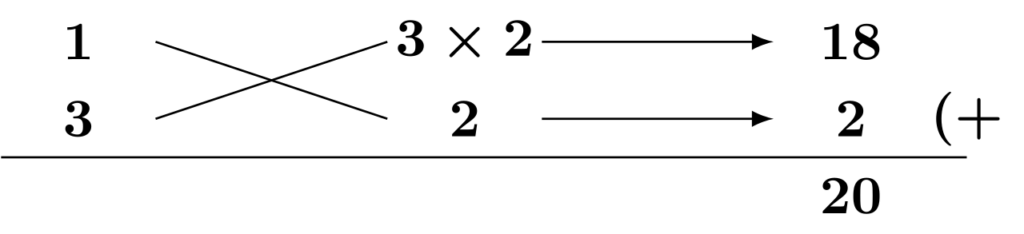
1次の係数$-20$と絶対値が合致しました。定数項を(負)×(負)にすれば完成です。
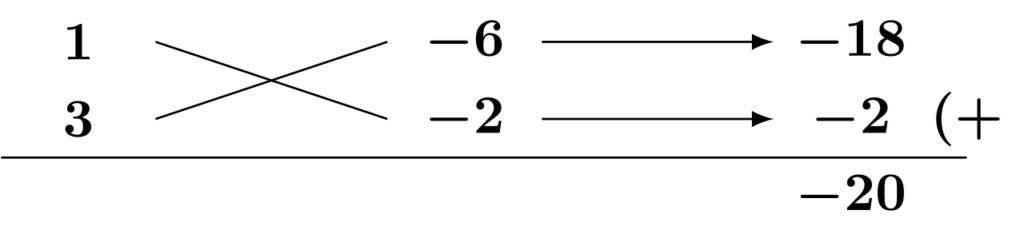
$$3x^2-20x+12=(x-6)(3x-2)$$
(2) $45x^2-39x-28$を因数分解します。
まずは、2次の係数と定数項(の絶対値)をそれぞれ素因数分解します。
$$\begin{gather}45=3^2\times 5\\28=2^2\times 7\end{gather}$$
2次の係数から考えていきましょう。ここで以下のことに注目します。
- 2次の係数が素因数$3$を2つ持っている
- 定数項が素因数$3$を持っていない
- 1次の係数が$3$の倍数である
もし、2次の係数の素因数$3$が2つとも上下のどちらか一方に固まっているとどうなるでしょうか。一例として以下の図を見てください。
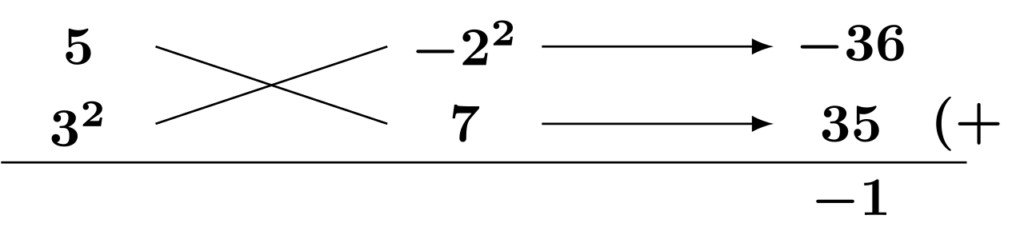
右上がりの積は素因数$3$が掛けられているので$3$の倍数である$-36$になっている一方、右下がりの積は素因数$3$が掛けられていないので$35$という$3$の倍数でない数になっています。たすき掛けの結果は$3$の倍数である$-36$と$3$の倍数でない$35$の和となり、その和$-1$は$3$の倍数ではありません。
上図の組み合わせ以外でも、素因数$3$を1つの段に固めている限り、他の素因数をどこに配置しようがたすき掛けの結果は$3$の倍数にはなりません。これは、斜めの積のうち、一方が$3$の倍数、もう一方が$3$の倍数でない数となり、その和は$3$の倍数ではないためです。
対して、素因数$3$を上下に1つずつ配置した場合はどうなるでしょうか。
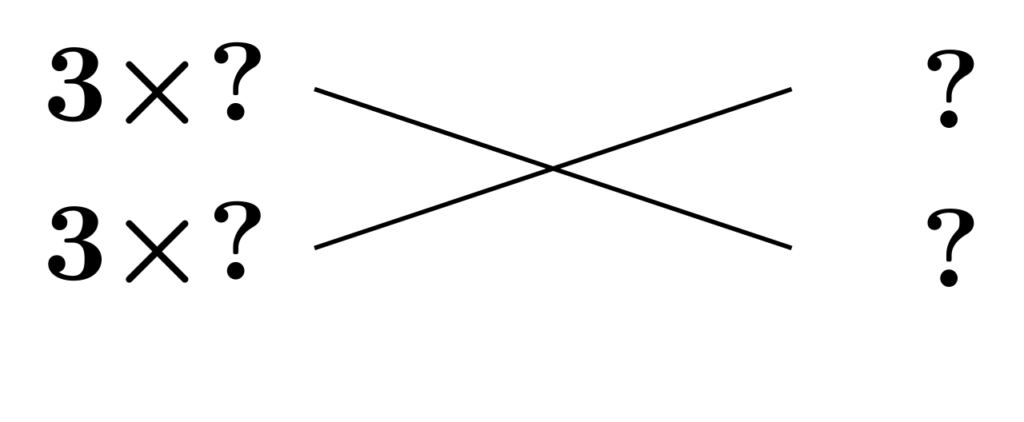
この場合、斜めの積は2つとも$3$の倍数です。よって、$3$の倍数どうしの和となることから、たすき掛けの結果も$3$の倍数となります。今回、1次の係数は$3$の倍数なので、この配置が適することになります。
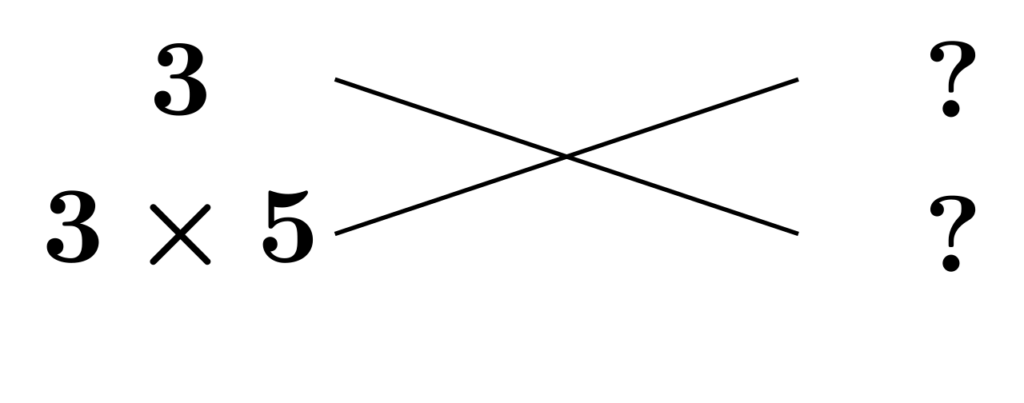
2次の係数は素因数$5$が残っていますが、上下どちらに置いても上下を入れ替えれば同一の組み合わせとなります。ここでは、当サイトのルール「上段よりも下段の数を大きくする」に従い、下段に配置することにします。
続いて、定数項の素因数の配置を考えます。ここでは、以下の点に着目します。
- 定数項が素因数$2$を2つ持っている
- 2次の係数が素因数$2$を持っていない
- 1次の係数が$2$の倍数ではない
先程の2次の係数のときの話を応用すると、
- 定数項がもつ2つの素因数$2$を上下のどちらか一方のみにすべて置く
→ たすき掛けの結果は$2$の倍数ではない - 定数項がもつ2つの素因数$2$を上下に1つずつ置く
→ たすき掛けの結果は$2$の倍数になる
ということが言えます。今回、1次の係数は$2$の倍数ではないので、前者のケースが採用されます。以上により、考えられる組み合わせは(定数項の符号を除いて)以下の4通りに絞られます。
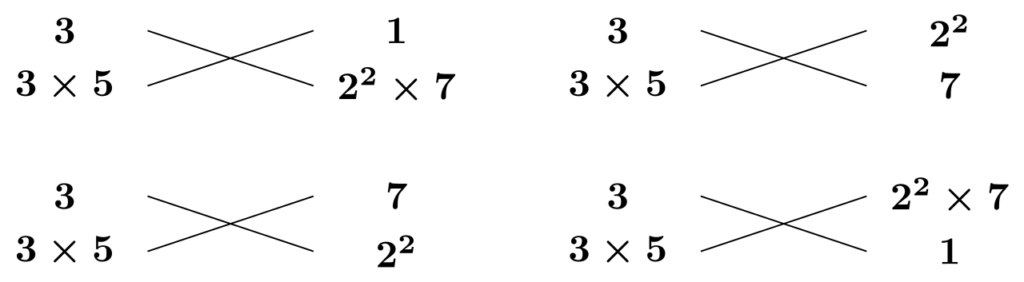
これらのうち適切なものを探すと、以下のようになります。
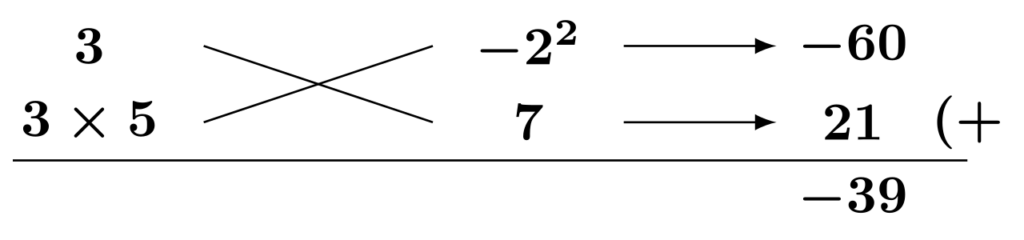
$$45x^2-39x-28=(3x-4)(15x+7)$$
何も考えずにたすき掛けをすると数十通りのパターンを考えないといかないところが4通りで済むので、計算効率アップに絶大な効果をもたらします。
習得は難しいですが、マスターすればかなり効率が上がるので、たすき掛けの基本的な手順が理解できたら試していきましょう。
これだけは覚えよう!図不要の瞬殺パターン
以下のパターンに遭遇したら、たすき掛けの図を書くことなく瞬殺してしまいましょう!
$$ax^2\pm (ab+1)x+b=(ax\pm 1)(x\pm b)\quad\textsf{(複号同順)}$$
[2次の係数]×[定数項]+1 と 1次の係数 の絶対値が等しいときに使う!
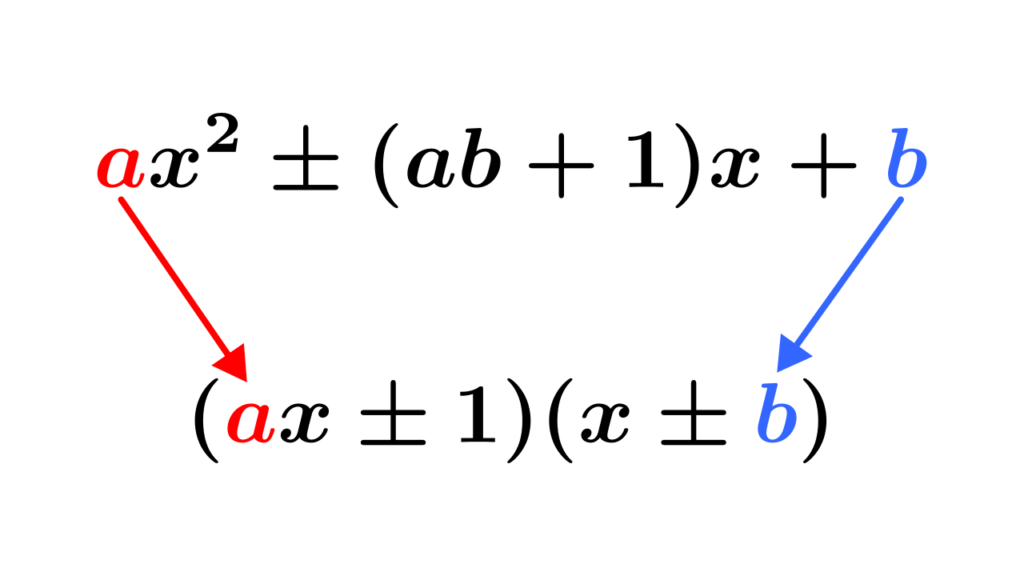
実際にたすき掛けをしたり、右辺を展開したりすることで成立が確かめられます。
「+」と「-」を合わせた「$\pm$」や「$\mp$」といった記号を複号と言います。1つの式の中に複号が複数出てくるとき、上にある記号どうし、下にある記号どうしの組み合わせのみを許容する場合を複号同順と言います。これに対し、上下の記号を自由に組み合わせられる場合を複号任意と言います。
(1) $4x^2+29x+7$を因数分解します。
[2次の係数]×[定数項]+1$=4\times 7+1=29=$[1次の係数]より、瞬殺パターン①に当てはまります。[2次の係数]×[定数項]+1 と 1次の係数 が等しい場合、複号はすべて+とします。
$$4x^2+29x+7=(4x+1)(x+7)$$
(2) $5x^2+39x-8$を因数分解します。
[2次の係数]×[定数項]+1$=5\times(-8)+1=-39$となり、1次の係数と符号のみ異なります。これも瞬殺パターン①に当てはまります。[2次の係数]×[定数項]+1 と 1次の係数 が符号のみ異なる場合、複号はすべて-とします。
$$5x^2+39x-8=(5x-1)\{x-(-8)\}=(5x-1)(x+8)$$
$$ax^2\pm (a+b)x+b=(x\pm 1)(ax\pm b)\quad\textsf{(複号同順)}$$
[2次の係数]+[定数項] と 1次の係数 の絶対値が等しいときに使う!
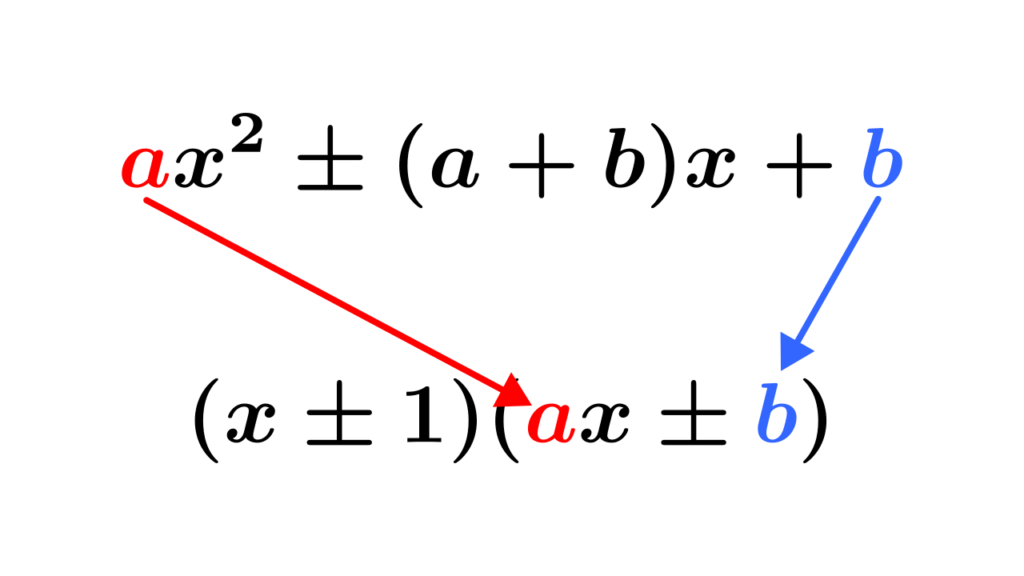
こちらもたすき掛けや右辺の展開で成立が確かめられます。
(1) $8x^2+3x-5$を因数分解します。
[2次の係数]+[定数項]$=8+(-5)=3=$[1次の係数]より、瞬殺パターン①に当てはまります。[2次の係数]+[定数項] と 1次の係数 が等しい場合、複号はすべて+とします。
$$8x^2+3x-5=(x+1)\{8x+(-5)\}=(x+1)(8x-5)$$
(2) $12x^2-37x+25$を因数分解します。
[2次の係数]+[定数項]$=12+25=37$となり、1次の係数と符号のみ異なります。これも瞬殺パターン①に当てはまります。[2次の係数]+[定数項] と 1次の係数 が符号のみ異なる場合、複号はすべて-とします。
$$12x^2-37x+25=(x-1)(12x-25)$$
最終目標:図を書かずにたすき掛け
たすき掛けをミスなく素早く解ける自信がついてきたら、たすき掛けの図を書かずに$([\quad]x+[\quad])([\quad]x+[\quad])$という状態の式を書き、空いている場所に直接数を入れて計算できるようになりましょう。
$n$乗+$n$乗、$n$乗-$n$乗の因数分解
$a^4-b^4$を因数分解し、その結果と以下の公式の共通点を述べよ。
$$\begin{align*}[\mathrm{C}]\quad&a^2-b^2=(a+b)(a-b)\\ [\mathrm{J}]\quad&a^3-b^3=(a-b)(a^2+ab+b^2)\end{align*}$$
$a^4-b^4$は因数分解の公式[C]によって因数分解できますね。
$$\begin{align*}&\hspace{1.3em}a^4-b^4\\&=(a^2+b^2)(a^2-b^2)\\&=(a^2+b^2)(a+b)(a-b)\end{align*}$$
さて、3つの式を見比べてみましょう。
$$\begin{align*}a^2-b^2&=(a-b)(a+b)\\a^3-b^3&=(a-b)(a^2+ab+b^2)\\a^4-b^4&=(a-b)(a+b)(a^2+b^2)\end{align*}$$
いずれの式も
- 左辺が$a$の◯乗-$b$の◯乗の形
- 右辺の因数に$a-b$が含まれる
という点が共通しています。
実は、以下の公式が成り立ちます。
$n$を$2$以上の整数とする。
$$a^n-b^n=(a-b)(a^{n-1}+a^{n-2}b+a^{n-3}b^2+\cdots +ab^{n-2}+b^{n-1})$$
右辺の2つ目の括弧にある「…」は「全部はとても書ききれないから前後の並びからパターンを読み取ってそれに従って上手いこと補完してね」という記号です。数や項が無限に続くときや、有限だけど個数が変化して定まらないときで、並びに規則性があるときに登場します。
今回の場合は、$a$の指数が$1$ずつ減っていくように、かつ$b$の指数が$1$ずつ増えていくように項を書き並べます。
公式より、
$$\begin{align*}a^2-b^2&=(a-b)(a+b)&n=2\,\textsf{のとき}\\a^3-b^3&=(a-b)(a^2+ab+b^2)&n=3\,\textsf{のとき}\\a^4-b^4&=(a-b)(a^3+a^2b+ab^2+b^3)&n=4\,\textsf{のとき}\\a^5-b^5&=(a-b)(a^4+a^3b+a^2b^2+ab^3+b^4)&n=5\,\textsf{のとき}\end{align*}$$
となります。
このように、$n$乗-$n$乗の形の式は$a-b$の因数を持つ形に因数分解することができます。注意しておきたいのは、この公式は必ずしも因数分解をやり尽くした形ではないということです。$\mathrm{THINK}$と例で$a^4-b^4$の因数分解の結果を見比べると、このことがわかると思います。
また、$n$乗+$n$乗の公式もあります。
$n$を$3$以上の奇数とする。
$$a^n+b^n=(a+b)(a^{n-1}-a^{n-2}b+a^{n-3}b^2-\cdots -ab^{n-2}+b^{n-1})$$
奇数乗のときにしか因数分解できないことに注意してください。
公式より、
$$\begin{align*}a^3+b^3&=(a+b)(a^2-ab+b^2)&n=3\,\textsf{のとき}\\a^5+b^5&=(a+b)(a^4-a^3b+a^2b^2-ab^3+b^4)&n=5\,\textsf{のとき}\end{align*}$$
となります。
公式の証明は右辺を展開すればできますし、数Ⅱで習う因数定理や等比数列の和の公式からも確認できます。
これらの公式は大学入試でもよく使うので、知っておいて損はないでしょう。
有理数の範囲を超えての因数分解
皆さんに質問です。$x^2-2$は因数分解することができるでしょうか?
多くの人はできないと思ったでしょう。一方、中には下のような変形を考えた人がいるかもしれません。
$$x^2-2=x^2-\qty(\sqrt{2\,})^2=\qty(x+\sqrt{2\,})\qty(x-\sqrt{2\,})$$
これは確かに立派な因数分解なのですが、根号が出てくることに少し戸惑うかもしれません。
普通、因数分解は係数が有理数の範囲で考えます。特に、元の式の係数がすべて整数のときは、因数も係数をすべて整数とするのが一般的です。しかし、上のように係数の範囲を実数に広げることでより多くの式を因数分解できるようになります。
さらに、数Ⅱで学習する複素数を用いると、2次以上の多項式は必ず1次式のみの積に因数分解できます。
$$3x^2+6x+7=3\qty(x+\frac{3+2\sqrt{3}\,i}{3})\qty(x+\frac{3-2\sqrt{3}\,i}{3})$$
では、実際のところどの範囲の数で因数分解するべきなのでしょうか。
通常は係数が有理数の範囲で因数分解をすれば十分です。「~を因数分解せよ」という問題は原則有理数の範囲での因数分解が要求されています。
実数の範囲や複素数の範囲での因数分解は必要なときだけ行います。方程式や不等式、多項式の関数について考えているシーンなどで要求されることがあります。
まとめ
- 楽に素早く計算する方法を常に考える癖をつけよう
- 同じ形はひとかたまりで考えよう
- 係数に注目して全く同じ項と符号だけが異なる項に分ける方法が効果的
- 展開の順番を工夫して項の数を増やさないようにしよう