ここでは、展開の際に簡単に素早く計算できる工夫について解説します。
楽に素早く計算する方法を常に考える癖をつけよう
数学において計算は常に必要となる作業です。高校数学では、計算も高度化し慎重に行わないとミスをしてしまうような複雑な計算もたくさん出てきます。だからこそ、数式の展開のような単純な計算はできるだけ楽に素早く計算したいものです。そのために、計算を楽にできる方法を知っておき、今自分ができる計算に適用できないかを常に考える習慣が重要です。このページで数式の展開における工夫を学んだら、今日から活用できるように意識して計算しましょう。
同じ形をひとかたまりと見る
次の式を展開せよ。$$(a+b+c+d)(a+b-c-d)$$
まずは、工夫せずにそのまま計算してみましょう。
$$\begin{align*}&\hspace{1.3em}(a+b+c+d)(a+b-c-d)\\&=a\cdot a+a\cdot b+a\cdot(-c)+a\cdot(-d)\\&\hspace{1.3em}+b\cdot a+b\cdot b+b\cdot(-c)+b\cdot(-d)\\&\hspace{1.3em}+c\cdot a+c\cdot b+c\cdot(-c)+c\cdot(-d)\\&\hspace{1.3em}+d\cdot a+d\cdot b+d\cdot(-c)+d\cdot(-d)\\&=a^2+ab-ac-ad+ba+b^2-bc-bd\\&\hspace{1.3em}+ca+cb-c^2-cd+da+db-dc-d^2\\&=a^2+b^2-c^2-d^2+2ab-2cd\end{align*}$$
1行目から2行目にかけての展開で16回の掛け算を行わなければならず面倒であることに加え、項が16個と多数出現するためにその後の同類項の整理でミスをする可能性も上がります。
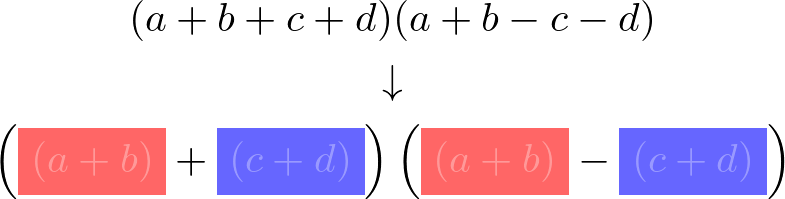
では、どう工夫すればよいでしょうか。展開前の式を見ると、それぞれの括弧の中の式が似ていることがわかります。具体的には、$a$と$b$は2つの式で係数が同じであるのに対し、$c$と$d$は係数が符号のみ逆になっています。そこで、符号が同じものと違うもので分け、次のように変形してみます。
$$(a+b+c+d)(a+b-c-d)=\{(a+b)+(c+d)\}\{(a+b)-(c+d)\}$$
$P=a+b,\,Q=c+d$とすると、$(P+Q)(P-Q)$となるので、次の展開の公式が利用できます。
$$[C]\quad (a+b)(a-b)=a^2-b^2$$
これを踏まえて計算してみましょう。
$$\begin{align*}&\hspace{1.3em}(a+b+c+d)(a+b-c-d)\\&=\{(a+b)+(c+d)\}\{(a+b)-(c+d)\}\end{align*}$$
$P=a+b,\,Q=c+d$とおくと、
〈答案の書き方〉置き換えするときは置き換え内容を文章で書く!
$$\begin{align*}&\hspace{1.3em}(P+Q)(P-Q)\\&=P^2-Q^2&\leftarrow 展開の公式[\mathrm{C}]の利用\\&=(a+b)^2-(c+d)^2\\&=(a^2+2ab+b^2)-(c^2+2cd+d^2)&\leftarrow 展開の公式[\mathrm{A}]の利用\\&=a^2+b^2-c^2-d^2+2ab-2cd\end{align*}$$
$$\begin{align*}展開の公式[\mathrm{C}]\quad&(a+b)(a-b)=a^2-b^2\\展開の公式[\mathrm{A}]\quad&(a+b)^2=a^2+2ab+b^2\end{align*}$$
このように計算すると、展開の大半を公式の利用で済ませることができるので、楽に計算することができます。
上の例では、一度$P,\,Q$に置き換えて計算しましたが、慣れてきたら置き換えをせずに計算でいるようになりましょう。頭の中で同じ形の部分を大枠で捉えるのがコツです。
$$\begin{align*}&\hspace{1.3em}(a+b+c+d)(a+b-c-d)\\&=(a+b)^2-(c+d)^2\\&=(a^2+2ab+b^2)-(c^2+2cd+d^2)\\&=a^2+b^2-c^2-d^2+2ab-2cd\end{align*}$$
同じ形は ひとかたまり
同じ形の部分は置き換えを利用するなどして、形を崩さないように計算しよう!
展開の順番を工夫する
次の式を展開せよ。$$(x-2)(x+1)(x+2)$$
この問題を2通りで解いてみます。解き方を比較して、どのような工夫をしているか考えてみましょう。
$$\begin{align*}&\hspace{1.3em}(x-2)(x+1)(x+2)\\&=\{x^2+(-2+1)x+(-2)\cdot 1\}(x+2)\qquad\leftarrow 展開の公式[\mathrm{D}]の利用\\&=(x^2-x-2)(x+2)\\&=x^2\cdot x+x^2\cdot 2+(-x)\cdot x+(-x)\cdot 2+(-2)\cdot x+(-2)\cdot 2\\&=x^3+2x^2-x^2-2x-2x-4\\&=x^3+x^2-4x-4\end{align*}$$
$$\begin{align*}展開の公式[\mathrm{D}]\quad&(x+a)(x+b)=x^2+(a+b)x+ab\end{align*}$$
$$\begin{align*}&\hspace{1.3em}(x-2)(x+1)(x+2)\\&=(x-2)(x+2)(x+1)\\&=(x^2-4)(x+1)\qquad\leftarrow 展開の公式[\mathrm{C}]の利用\\&=x^2\cdot x+x^2\cdot 1+(-4)\cdot x+(-4)\cdot 1\\&=x^3+x^2-4x-4\end{align*}$$
$$\begin{align*}展開の公式[\mathrm{C}]\quad&(a+b)(a-b)=a^2-b^2\end{align*}$$
どちらも公式を活用しながら展開していますが、「良くない例」では3行目から4行目にかけての計算で6回の掛け算を要しているのに対し、「良い例」では4回で済んでいます。前者は公式[D]を利用したため、公式を利用した部分が項が3つの式になっていますが、後者では掛け算の順番を変えて公式[C]を利用したことで項が2つに抑えられています。項が減ればその後の計算が楽になります。
このように、展開の順番を工夫することで楽に計算できる場合があります。ポイントは項の数をできるだけ増やさないことです。次の3つの公式は展開後の式の項が少ないので、これらの公式が使える掛け算の組がある場合は優先的に計算するようにしましょう。
$$\begin{align*}展開の公式[\mathrm{C}]\quad&(a+b)(a-b)=a^2-b^2\\展開の公式[\mathrm{I}]\quad&(a+b)(a^2-ab+b^2)=a^3+b^3\\展開の公式[\mathrm{J}]\quad&(a-b)(a^2+ab+b^2)=a^3-b^3\end{align*}$$
練習問題
上記の工夫を活用して楽に計算するように意識しましょう。
問題
次の式を計算せよ。$$\begin{align*}(1)\quad&(p^2+4q^2)(p+2q)(p-2q)\\(2)\quad&(3x+4y-5z)(3x-4y+5z)\\(3)\quad&(x^2-6x+4)(x^2+3x+4)\\(4)\quad&(a+b)^2(a-b)^2\\(5)\quad&(x^2-4x+16)(x^2+2x+4)(x+4)(x-2)\\(6)\quad&(x+1)(x+2)(x+3)(x+4)\\(7)\quad&(x+y-z)^2+(y+z-x)^2+(z+x-y)^2+(x+y+z)^2\end{align*}$$
解説
(1) 後ろの2つの式から展開すると、公式[C]を利用できます。
$$\begin{align*}&\hspace{1.3em}(p^2+4q^2)(p+2q)(p-2q)\\&=(p^2+4q^2)\{p^2-(2q)^2\}\quad\leftarrow 公式[\mathrm{C}]\\&=(p^2+4q^2)(p^2-4q^2)\\&=\qty(p^2)^2-\qty(4q^2)^2\quad\leftarrow 公式[\mathrm{C}]\\&=p^4-16q^4\end{align*}$$
$$\begin{align*}展開の公式[\mathrm{C}]\quad&(a+b)(a-b)=a^2-b^2\end{align*}$$
(2) 2つの式で符号が同じ項と符号が異なる項に分け、符号が異なる項は一方をマイナスでくくりましょう。
$$\begin{align*}&\hspace{1.3em}(3x+4y-5z)(3x-4y+5z)\\&=\{3x+(4y-5z)\}\{3x-(4y-5z)\}\\&=(3x)^2-(4y-5z)^2\quad\leftarrow 公式[\mathrm{C}]\\&=9x^2-(16y^2-40yz+25z^2)\quad\leftarrow 公式[\mathrm{B}]\\&=9x^2-16y^2-25z^2+40yz\end{align*}$$
$$\begin{align*}展開の公式[\mathrm{C}]\quad&(a+b)(a-b)=a^2-b^2\\展開の公式[\mathrm{B}]\quad&(a-b)^2=a^2-2ab+b^2\end{align*}$$
(3) $x^2,\,4$の2項が共通なので、ひとまとめにします。
$$\begin{align*}&\hspace{1.3em}(x^2-6x+4)(x^2+3x+4)\\&=\{(x^2+4)-6x\}\{(x^2+4)+3x\}\end{align*}$$
すると、少々わかりにくいですが、公式[D]が利用できる形になっています。$x$を$(x^2+4)$に、$a$を$-6x$に、$b$を$3x$に置き換えてください。
$$\begin{align*}&\hspace{1.3em}\{(x^2+4)-6x\}\{(x^2+4)+3x\}\\&=(x^2+4)^2+(-6x+3x)(x^2+4)+(-6x)\cdot 3x\quad\leftarrow 公式[\mathrm{D}]\\&=(x^4+8x^2+16)+(-3x)(x^2+4)-18x^2\quad\leftarrow 公式[\mathrm{A}](1つ目の括弧)\\&=x^4+8x^2+16-3x^3-12x-18x^2\\&=x^4-3x^3-10x^2-12x+16\end{align*}$$
$$\begin{align*}展開の公式[\mathrm{D}]\quad&(x+a)(x+b)=x^2+(a+b)x+ab\\展開の公式[\mathrm{A}]\quad&(a+b)^2=a^2+2ab+b^2\end{align*}$$
(4) 指数法則を使って2乗を1つにまとめると、公式[C]を利用できます。
$$\begin{align*}&\hspace{1.3em}(a+b)^2(a-b)^2\\&=\{(a+b)(a-b)\}^2\\&=\qty(a^2-b^2)^2\quad\leftarrow 公式[\mathrm{C}]\\&=a^4-2a^2b^2+b^4\quad\leftarrow 公式[\mathrm{B}]\end{align*}$$
$$\begin{align*}展開の公式[\mathrm{C}]\quad&(a+b)(a-b)=a^2-b^2\\展開の公式[\mathrm{B}]\quad&(a-b)^2=a^2-2ab+b^2\end{align*}$$
(5) 公式[I]および公式[J]が使える形に気付けましたか?
$$\begin{align*}&\hspace{1.3em}(x^2-4x+16)(x^2+2x+4)(x+4)(x-2)\\&=(x+4)(x^2-4x+16)\cdot (x-2)(x^2+2x+4)\\&=(x^3+4^3)(x^3-2^3)\quad\leftarrow 公式[\mathrm{I}](前半)\,および\,公式[\mathrm{J}](後半)\\&=(x^3+64)(x^3-8)\\&=\qty(x^3)^2+(64-8)x^3+64\cdot(-8)\quad\leftarrow 公式[\mathrm{D}]\\&=x^6+56x^3-512\end{align*}$$
$$\begin{align*}展開の公式[\mathrm{I}]\quad&(a+b)(a^2-ab+b^2)=a^3+b^3\\展開の公式[\mathrm{J}]\quad&(a-b)(a^2+ab+b^2)=a^3-b^3\\展開の公式[\mathrm{D}]\quad&(x+a)(x+b)=x^2+(a+b)x+ab\end{align*}$$
(6) 一見工夫のしようがないように見えますが、次の手順で展開すると同じ形を出現させることができます。
$$\begin{align*}&\hspace{1.3em}(x+1)(x+2)(x+3)(x+4)\\&=(x+1)(x+4)\cdot (x+2)(x+3)\\&=(x^2+5x+4)(x^2+5x+6)\quad\leftarrow 公式[\mathrm{D}]\\&=\{(x^2+5x)+4\}\{(x^2+5x)+6\}\\&=(x^2+5x)^2+(4+6)(x^2+5x)+4\cdot 6\quad\leftarrow 公式[\mathrm{D}]\\&=\qty{\qty(x^2)^2+2\cdot x^2\cdot 5x+(5x)^2}+10(x^2+5x)+24\quad\leftarrow 公式[\mathrm{A}](1つ目の括弧)\\&=x^4+10x^3+25x^2+10x^2+50x+24\\&=x^4+10x^3+35x^2+50x+24\end{align*}$$
1回目の公式[D]の利用の際に、和$a+b$か積$ab$のいずれかが同じになるように掛け算の組み合わせを決めるのがコツです。今回の場合は、和が$5$になる組み合わせを2組作りました。
$$\begin{align*}展開の公式[\mathrm{D}]\quad&(x+a)(x+b)=x^2+(a+b)x+ab\\展開の公式[\mathrm{A}]\quad&(a+b)^2=a^2+2ab+b^2\end{align*}$$
(7) 2乗をすべてばらしてしまうと面倒です。どれか2つの括弧に着目すれば、係数が同じ項と符号だけ違う項に分ける考え方が利用できます。ここでは、前2つと後ろ2つに分けて計算してみましょう。まずは前2つの計算です。
$$\begin{align*}&\hspace{1.3em}(x+y-z)^2+(y+z-x)^2\\&=\{y+(x-z)\}^2+\{y-(x-z)\}^2\\&=\{y^2+2y(x-z)+(x-z)^2\}+\{y^2-2y(x-z)+(x-z)^2\}\quad\leftarrow 公式[\mathrm{A}](前半)\,および\,公式[\mathrm{B}](後半)\\&=2y^2+2(x-z)^2\end{align*}$$
次に後ろ2つの計算です。
$$\begin{align*}&\hspace{1.3em}(z+x-y)^2+(x+y+z)^2\\&=\{(x+z)-y\}^2+\{(x+z)+y\}^2\\&=\{(x+z)^2-2(x+z)y+y^2\}+\{(x+z)^2+2(x+z)y+y^2\}\quad\leftarrow 公式[\mathrm{B}](前半)\,および\,公式[\mathrm{A}](後半)\\&=2(x+z)^2+2y^2\end{align*}$$
よって、まとめると次のようになります。
$$\begin{align*}&\hspace{1.3em}(x+y-z)^2+(y+z-x)^2+(z+x-y)^2+(x+y+z)^2\\&=2y^2+2(x-z)^2+2(x+z)^2+2y^2\\&=4y^2+2(x^2-2xz+z^2)+2(x^2+2xz+z^2)\quad\leftarrow 公式[\mathrm{B}]\qty((x-z)^2)\,および\,公式[\mathrm{A}]\qty((x+z)^2)\\&=4y^2+2x^2-4xz+2z^2+2x^2+4xz+2z^2\\&=4x^2+4y^2+4z^2\end{align*}$$
$$\begin{align*}展開の公式[\mathrm{A}]\quad&(a+b)^2=a^2+2ab+b^2\\展開の公式[\mathrm{B}]\quad&(a-b)^2=a^2-2ab+b^2\end{align*}$$
解答
$$\begin{align*}(1)\quad&p^4-16q^4\\(2)\quad&9x^2-16y^2-25z^2+40yz\\(3)\quad&x^4-3x^3-10x^2-12x+16\\(4)\quad&a^4-2a^2b^2+b^4\\(5)\quad&x^6+56x^3-512\\(6)\quad&x^4+10x^3+35x^2+50x+24\\(7)\quad&4x^2+4y^2+4z^2\end{align*}$$
まとめ
- 楽に素早く計算する方法を常に考える癖をつけよう
- 同じ形はひとかたまりで考えよう
- 係数が同じ項と符号だけが異なる項に分ける方法が効果的
- 展開の順番を工夫して項の数を増やさないようにしよう
